Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 12

Os problemas a seguir, se referem a um perfil de aço laminado selecionado em um problema do capítulo 5, para suportar determinado carregamento a um custo mínimo e ao mesmo tempo satisfazendo a condição σ m ≤ σ a d m . Para o projeto selecionado, determine (a) o valor real de σ m na viga e (b) o valor máximo de σ a d m na junção de uma mesa com alma.

“carregamento do problema 5.76 e perfil S 15 × 42,9 selecionado”:

Passo 1

Então gurizada, vamos começar logo?! iniciemos com nossos cálculos:

Dados do problema 5.76: σ t u d o = 24   k s i

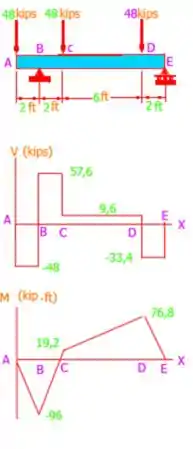
V = 38,4   k i p s M t o t a l = 96   k i p × f t = 1152   k i p × i n em D

Passo 2

Para seção S 15 × 42,9 de aço laminado:

d = 15,0   i n b f = 5,50   i n t f = 0,622   i n t w = 0,411   i n

I z = 44 6   i n 4 S z = 59,4   i n 3 c = 1 2 d = 7,5   i n

(a) σ m = M t o t a l S z = 1152 59,4 = 19,3939   k s i

Passo 3

Temos que?

y b = c - t f = 6,878   i n

σ b = y b c σ m = 17,7855   k s i σ b 2 = 8,8928   k s i

A f = b f t f = 3,421   i n 2

y _ = 1 2 c + y b = 7,189   i n

Q b = A f y _ f = 24,594   i n 3

τ b = V Q I z t w = ( 57,6 ) ( 24,594 ) ( 446 ) ( 0,411 ) = 7,7281   k s i

R = ( σ b 2 ) 2 + τ b 2 = 8,8928 2 + 7,7281 2 = 11,7816   k s i

σ t o t a l = σ b 2 + R = 8,8928 + 11,7816 = 20,7   k s i

Resposta

( a )             σ m = 19,39   k s i

(b) σ t o t a l = 20,7   k s i .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

26. A viga T está sujeita ao carregamento distribuído aplicado ao longo de sua linha central. Determine as tensões principais nos pontos A e B e mostre os resultados em elementos localizados em cada u
28. A superfície da viga simplesmente apoiada está sujeita à tensão de tração τ 0 . Determine as tensões principais nos pontos A e B .
27. A haste curvada tem diâmetro de 15m m e está sujeita à força de 600N . Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto A e no ponto B . Mostre os
29. A viga tem seção transversal retangular e está sujeita às cargas mostradas. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto A e no ponto B. Esses
34. O eixo tem diâmetro d e está sujeito às cargas mostradas. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto A. Os mancais suportam apenas reações ve