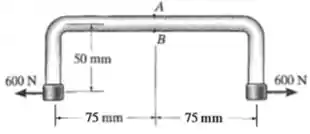
27. A haste curvada tem diâmetro de e está sujeita à força de . Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto e no ponto . Mostre os resultados em elementos adequadamente orientados nesses pontos.
Passo 1
Primeiro, vamos montar o seguinte esquema para o cálculo de força e momento:
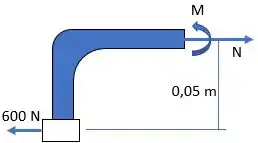
Basicamente, transpomos a força de para o ponto (ou ) da haste lembrando de adicionar o momento correspondente à transposição da força.
Agora, faremos as contas para achar o valor de N e M:
Passo 2
Como nossos cálculos anteriores são comuns aos dois pontos, iremos dividir a questão, resolvendo primeiro que foi pedido para o ponto e depois para o ponto .
Vamos fazer o cálculo da tensão no ponto , lembrando que o momento de inércia do círculo é dado por , onde é a distância do centro à borda do círculo:
Passo 3
Agora, calcularemos as tensões normais de superfície pela fórmula:
Com isso obtemos duas tensões, e :
Passo 4
Agora, vamos calcular a tensão de cisalhamento máxima no plano pela seguinte fórmula:
Passo 5
Neste passo, vamos encontrar o ângulo que o elemento será rotacionado:
E devemos calcular o arco tangente do valor encontrado:
Esse ângulo é quanto um dos eixos está deslocado. Para achar o outro ângulo , devemos somar noventa graus com :
Passo 6
Agora, vamos utilizar a fórmula a seguir para calcular a tensão deslocada no nosso elemento:
Passo 7
Por fim, calcularemos a tensão média :
Passo 8
Aqui, repetiremos todos os passos anteriores para o ponto .
Cálculo da tensão no ponto :
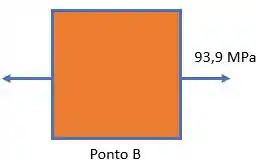
Passo 9
O cálculo das tensões normais de superfície pela fórmula:
Onde novamente obtemos duas tensões e :
Passo 10
Agora, calculemos a tensão de cisalhamento máxima no plano :
Passo 11
E em seguida, encontraremos o ângulo que o elemento será rotacionado:
E devemos calcular o arco tangente do valor encontrado:
Esse ângulo é quanto um dos eixos está deslocado. Já sabemos que para encontrar o outro, devemos somar noventa graus com :
Passo 12
E agora, vamos fazer o cálculo da tensão deslocada:
Passo 13
E por fim, calcularemos a tensão média :
Resposta
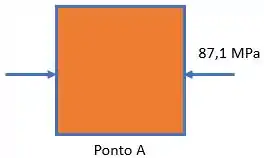
Tensões principais no ponto :
Tensão de cisalhamento máxima no ponto :

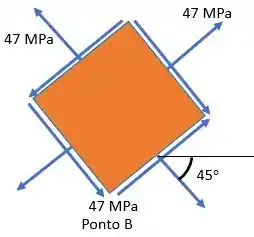
Tensões principais no ponto :
Tensão de cisalhamento máxima no ponto :