Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 83
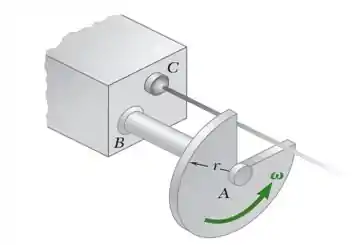
O obturador mostrado na figura foi formado removendo-se um quarto de um disco de 20 mm de raio e é usado para interromper um feixe de luz emitido a partir de uma lente em C. Sabendo que o obturador tem massa de 50 g e gira à taxa constante de 24 ciclos por segundo, determine a intensidade da força exercida pelo obturador sobre o eixo em A.
Passo 1
Falaaa... beleuza??
Antes de tudo a gente já repara que o centro de massa não está em A, certo?
Então a gente pode ir na tabela de centroides e pegar do setor circular:
Mas a nossa figura é:
E como para o círculo todo nós temos , então pra do círculo temos .
Daí podemos achar o nosso :
Detalheee que esse é o ângulo, heim? NÃO é aceleração angular.
Passo 2
Para o centróide de um setor circular.
Passo 3
Força no eixo é:
Magnitude
Resposta
Exercícios de Livros Relacionados
No instante t = 10s , a velocidade de uma partícula que se desloca no plano x - y é v = 0,1i + 2jm / s . No instante t = 10,1s , sua velocidade torna-se - 0,1i + 1,8jm / s . Determine o módulo a m é d
Uma partícula que se desloca em um movimento bidimensional tem coordenadas em milímetros dadas por x = t 2 - 4 t + 20 e y = 3s e n ( 2 t ) , onde t é o tempo em segundos. Determine os módulos da veloc
Para um determinado intervalo de movimento o pino A é forçado a se deslocar na ranhura fixa parabólica pelo braço horizontal com encaixe que é elevado na direção y a uma taxa constante de 30m m / s .
A partícula P se desloca ao longo da ranhura curva, uma parte desta é mostrada. Sua distância em metros medida ao longo da ranhura é dada por s = t 2 / 4 , onde t é em segundos. A partícula está em A
Uma partícula que se move em um movimento curvilíneo tem coordenadas em milímetros que variam com o tempo t em segundos de acordo com x = 3 t 2 - 4 t e y = 4 t 2 - 1 3 t 3 . Determine os módulos da ve