Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 26
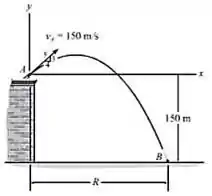
Um projétil é disparado com uma velocidade inicial de m/s do telhado do prédio. Determine o alcance R onde ele atinge o solo em B.
Passo 1
Utilizando a equação horária do espaço para MRUV
Substituindo os valores, teremos
Resolvendo a equação de 2° grau
s
Para o cálculo de
m
Resposta
O alcance será de 2386,37 m
Exercícios de Livros Relacionados
Prove o resultado de conhecimento geral que, para uma dada velocidade de lançamento v 0 , o ângulo de lançamento θ = 45 ° fornece a máxima distância horizontal R . Determine o alcance máximo. (Note qu
O centro de massa G de um atleta de salto em altura segue a trajetória mostrada. Determine a componente v 0 , medida no plano vertical da figura, da sua velocidade de impulsão e o ângulo θ se o ápice
Os movimentos x e y das guias A e B com ranhuras em ângulo reto controlam o movimento curvilíneo do pino P de conexão, que desliza nas duas ranhuras. Por um curto intervalo de tempo, os movimentos são
As coordenadas retangulares de uma partícula que se desloca no plano x - y são dadas por x = 3 cos ( 4 t ) e y = 2s e n ( 4 t ) , onde o tempo t é expresso em segundos e x e y são expressos em metro
Se o tenista mostrado na figura dá o saque com uma velocidade v de 130k m / h em um ângulo θ = 5 ° , calcule a folga vertical h do centro da bola acima da rede e a distância s a partir da rede onde a