Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 101

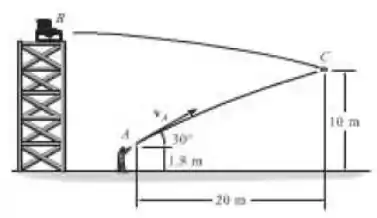
Um projétil é disparado da plataforma em B. O atirador realiza o disparo da sua arma do ponto A a um ângulo de 30°. Determine a velocidade escalar da bala na boca da arma se ela atinge o projétil em C.

Passo 1

Temos um problema de lançamento oblíquo. Um projétil percorrerá uma distância no plano x y . Calma. Podemos dividir este problema em dois outros problemas: um no eixo x e outro no eixo y . No eixo x a velocidade é constante e no eixo y a partícula está sujeita a ação da gravidade. Portanto, vamos analisar cada caso separadamente!

Passo 2

Precisamos determinar a velocidade escalar da bala. Para isto, vamos começar analisando o movimento dela no eixo x . Utilizando as equações da cinemática, teremos:

s = s 0 + v x t

20 = 0 + v A ⋅ cos ⁡ 30 ° t

t = 20 v A ⋅ cos ⁡ 30 °

t = 40 3 3 v A

Portanto, obtemos uma relação entre o tempo necessário para o projétil percorrer a distância de 20 m e a sua velocidade escalar. Precisamos agora analisar o seu movimento na direção do eixo y .

Passo 3

Vamos analisar o seu deslocamento no eixo y . Mas calma lá, muito cuidado nesta hora!!! A posição final do projétil será s = 10   m . E a posição inicial? s 0 = 0   m ??? Não! A resposta é simples e clara, não! Olhem o desenho com calma e percebam que s 0 = 1,8   m . Isto é, o projétil não parte do solo. Agora sim, utilizando as equações da cinemática, temos:

s = s 0 + v y t + a t 2 2

10 = 1,8 + v A ⋅ sen ⁡ 30 ° ⋅ t - g t 2 2

8,2 = v A ⋅ 20 3 3 v A - 4,905 ⋅ 40 3 3 v A 2

4,905 ⋅ 4800 9 v A 2 = 20 3 3 - 8,2  

3,347 v A 2 = 4,905 ⋅ 4800

Como a velocidade só pode ser positiva, pois caso contrário ela teria sentido contrário (ao invés de subir, ela desceria, o que não faz sentido para o nosso problema), temos:

v A = 27,96   m / s

Resposta

v A = 27,96   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pacotes pequenos movendo-se sobre uma esteira transportadora caem dentro de um carrinho de carga de 1 m de comprimento. Se a esteira está se movendo com uma velocidade escalar constante de v c = 2m /
Uma bola de futebol americano é chutada sobre o poste do gol com uma velocidade de v A = 24m / s como mostrado. Determine o ponto Bx , y onde ela atinge as arquibancadas.
A velocidade do jato de água saindo do orifício pode ser obtida de v = 2 g h , onde h = 2m é a distância do orifício até a superfície livre da água. Determine o tempo para uma partícula de água deixan
Uma bola de golfe é batida com uma velocidade de 24m / s , como mostrado. Determine a distância d medida do lançamento até o ponto B.