Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 108

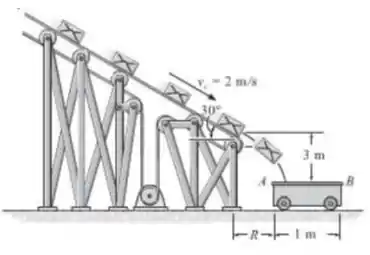
Pacotes pequenos movendo-se sobre uma esteira transportadora caem dentro de um carrinho de carga de 1 m de comprimento. Se a esteira está se movendo com uma velocidade escalar constante de v c = 2   m / s , determine a menor e a maior distância R na qual a extremidade A do carro possa ser colocada em relação à esteira de maneira que os pacotes entrem no carrinho.

Passo 1

Este é um problema interessante. A questão já nos deixa claro que existe um valor máximo e um valor mínimo da distância R para que os pacotes caiam no carrinho. Considerando um pacote como uma partícula e analisando a geometria do nosso problema, podemos imaginar que o comprimento máximo é aquele que faça com que o pacote caia exatamente na extremidade A do carrinho. Já a distância mínima nada podemos afirmar.

Para resolvermos esta questão, vamos calcular inicialmente o tempo de queda da partícula. Com este tempo, vamos descobrir qual a distância percorrida na direção do eixo x e assim, analisaremos os possíveis casos devido a este resultado.

Passo 2

Calcularemos inicialmente o tempo de queda do nosso pacote. Como ele está sujeito a ação da gravidade na direção do eixo y , temos a seguinte equação da cinemática:

s = s 0 + v y t + a t 2 2

- 3 = 0 - v A ⋅ sen ⁡ θ ⋅ t - g t 2 2

- 3 = - 2 ⋅ sen ⁡ 30 ° ⋅ t - 4,905 t 2

4,905 t 2 + t - 3 = 0

Resolvendo esta equação do segundo grau, obtemos t = 0,6867   s . Observem que o tempo tem que ser maior do que zero, por isto obtemos apenas um único resultado.

Passo 3

Com o valor do tempo descoberto no Passo 2, vamos determinar a distância percorrida no eixo x . Para isto, como não há presença de nenhuma aceleração, temos:

s = s 0 + v x t

s = 0 + v A ⋅ cos ⁡ 30 ° t

s = 2 ⋅ 3 2 ⋅ 0,6867

s = 1,19   m

Passo 4

Temos que determinar agora os valores máximos e mínimos de R para que o pacote caia no carrinho. Como já foi explicado no Passo 1, o valor máximo implica que o pacote caia exatamente na extremidade. Para que isto ocorra, o valor de R deve ser exatamente igual ao valor calculado no Passo 3, isto é:

R m á x = s = 1,19   m

Já se queremos determinar o valor mínimo, devemos resolver a seguinte relação:

R m í n + 1 = s = 1,19

R m í n = 0,19   m

Resposta

R m í n = 0,19   m

R m á x = 1,19   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se ao longo da trajetória circular de A para B em 1 s. Se ela leva 3 s para ir de A para C, determine a sua velocidade média quando ela vai de B para C.
O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de a t B = 0,5 e tm / s 2 , onde t é dado em segundos. Se um carro parte do repouso quando θ = 0 ° , determine as
O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de a t B = 0,5 e tm / s 2 , onde t é dado em segundos. Se um carro parte do repouso quando θ = 0 ° , determine as
Um barco está se movendo ao longo da trajetória circular com uma velocidade escalar de v = 0,0625 t 2m / s , onde t é dado em segundos. Determine a intensidade da sua aceleração quando t = 10s .
Quando x = 3m , o caixote tem uma velocidade escalar de 6m / s que está aumentando a 1,8m / s 2 . Determine a direção da velocidade do caixote e a intensidade da aceleração do caixote nesse instante.