9. Uma partícula move-se ao longo de uma pista reta de tal maneira que sua posição é descrita pelo gráfico s-t. Construa o gráfico v –t para o mesmo intervalo de tempo.
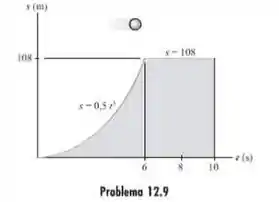
Passo 1
Para encontrar a velocidade da partícula temos que usar a seguinte equação,
Para substituindo, para s na equação mostrada acima,
Encontre a velocidade no ponto em que o tempo é 6 s (velocidade máxima),
Passo 2
Para substituindo108 para s na equação da velocidade,
O gráfico é plotado com base nos dados, conforme mostrado abaixo:
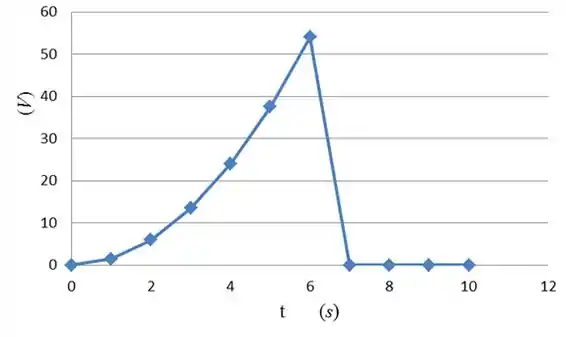
Nota: Aqui, a dose do gráfico não cai diretamente zero, pois nesse caso a desaceleração seria infinita, o que é praticamente impossível. Mas, nos casos ideais, essa queda pode ser considerada como linha vertical.
Resposta
Gráfico.