Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 104

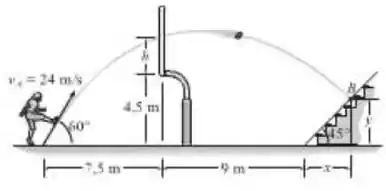
Uma bola de futebol americano é chutada sobre o poste do gol com uma velocidade de v A = 24   m / s como mostrado. Determine o ponto B   x , y onde ela atinge as arquibancadas.

Passo 1

Temos um problema de lançamento oblíquo! A bola possuirá componentes x e y da velocidade. Na direção y , temos a ação da gravidade. É por sua causa que a bola possui uma trajetória arqueada, subindo e posteriormente descendo. Já na direção do eixo x ela possui velocidade constante.

Precisamos determinar inicialmente o tempo t necessário para que a bola percorra a distância de (7,5+9+x) m na direção do eixo x , e assim, chegará na posição das arquibancadas. Com este valor do tempo, utilizaremos na equação da cinemática na direção do eixo y , a fim de descobrir a posição da bola.

Passo 2

Vamos começar determinando o tempo t . Na direção do eixo x temos:

s = s 0 + v x t

16,5 + x = 0 + v A cos ⁡ 60 ° t

16,5 + x = 12 t

Portanto, conseguimos uma relação do tempo com a distância x .

Passo 3

Agora, vamos resolver a equação da posição da bola na direção do eixo y . Desta forma, temos:

s = s 0 + v y t + a t 2 2

y = 0 + v A ⋅ sen ⁡ 60 ° ⋅ t - g t 2 2

y = 12 3 t - 4,905 t 2

Portanto, obtemos uma relação do tempo com a posição y . Substituindo nesta equação a relação descrita no Passo 1, temos:

y = 12 3 ⋅ 16,5 + x 12 - 4,905 ⋅ 16,5 + x 2 12 2

12 2 y = 144 3 ⋅ 16,5 + x - 4,905 ⋅ 16,5 + x 2

144 y = - 4,905 x 2 + 87,55 x + 2780

Agora, obtemos uma equação que relaciona as posições x e y da nossa bola.

Passo 4

Precisamos encontrar uma nova relação entre as posições x e y para que possamos resolver o nosso problema. Para isto, precisaremos utilizar a relação geométrica do nosso problema. Nele, temos um tri��ngulo retângulo tal que:

tan ⁡ 45 ° = y x = 1

Portanto, y = x . Substituindo esta relação na equação do Passo 3, teremos:

144 y = - 4,905 x 2 + 87,55 x + 2780

4,905 x 2 + 56,45 x - 2780 = 0

x 2 + 11,5 x - 566,7 = 0

Resolvendo esta equação, obtemos x 1 = - 30,2   m e x 2 = 18,8   m . Como o valor negativo não faz sentido para o nosso problema, temos que a posição x e a posição y do ponto B são 18,8   m . Portanto, B   ( 18,8 ; 18,8 ) .

Resposta

B   ( 18,8 ; 18,8 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o carro desacelera uniformemente ao longo da estrada curva de 25m / s em A para 15m / s em C, determine a aceleração do carro em B.
O carro sobe um morro com uma velocidade escalar de v = 0,2 sm / s , onde s é dado em metros, medido a partir de A. Determine a intensidade da sua aceleração quando ele está no ponto s = 50m , onde ρ
Se a motocicleta tem uma desaceleração de a t = - 0,001 sm / s 2 e sua velocidade escalar na posição A é 25m / s , determine a intensidade da sua aceleração quando ela passa o ponto B.
Um carro está se movendo ao longo da estrada com a velocidade escalar de v = ( 300 / s )m / s , onde s é dado em metros. Determine a intensidade da sua aceleração quando t = 3s se t = 0 em s = 0 .
Uma partícula move-se ao longo da trajetória parabólica y = b x 2 . Se sua componente da velocidade ao longo do eixo y é v y = c t 2 , determine as componentes x e y da aceleração da partícula. Aqui,