Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 93

Um projétil é disparado com uma velocidade u perpendicular ao declive, que está inclinado de um ângulo θ com a horizontal. Derive uma expressão para a distância R até o ponto de impacto.

Passo 1

Pessoa, será necessário construirmos aqui a equação da trajetória desse projétil, ou seja, uma equação de y em função de x e de outras constantes, mas não do tempo.

Começamos pela seguinte equação do movimento horizontal:

x = x 0 + v x t = x 0 + u cos ⁡ α t

t = x - x 0 v 0 cos ⁡ α

onde α será o ângulo de lançamento em relação à horizontal.

Agora, a gente escreve a seguinte equação do movimento vertical:

y = y 0 + v 0 y t - 1 2 g t 2 = y 0 + u   s e n   α t - 1 2 g t 2

Só resta substituir a expressão de t já encontrada:

y = y 0 + u   s e n   α x - x 0 u cos ⁡ α - 1 2 g x - x 0 u cos ⁡ α 2

y = y 0 + t g   α x - x 0 - g sec 2 ⁡ α 2 u 2 x - x 0 2

Essa é a equação da trajetória!

Passo 2

Agora, vamos considerar que a origem do nosso sistema de coordenadas esteja justamente no ponto de impacto. Então teremos:

x 0 = - R cos ⁡ θ

y 0 = R   s e n   θ

Além disso, precisamos relacionar os ângulos θ e α . Olhe pra seguinte figura:

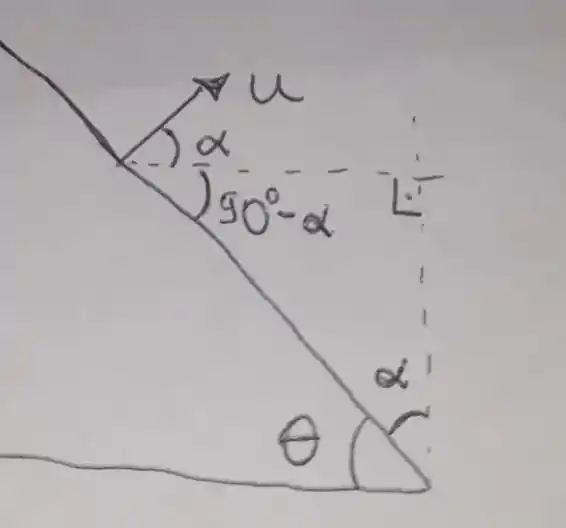
Aqui vemos que θ + α = 90 ° , logo:

α = 90 ° - θ

s e n   α = cos ⁡ θ

cos ⁡ α = s e n   θ

t g   α = c o t g   θ

sec ⁡ α = c o s s e c   θ

Passo 3

Agora, usaremos todos os dados obtidos no passo anterior para substituir na equação da trajetória obtida:

y = y 0 + t g   α x - x 0 - g sec 2 ⁡ α 2 u 2 x - x 0 2

Também já vamos substituir o ponto x ,   y = ( 0 ,   0 ) , que é o ponto de impacto:

0 = R   s e n   θ + c o t g   θ 0 - - R cos ⁡ θ - g   c o s s e c 2 θ 2 u 2 0 - - R cos ⁡ θ 2

0 = R   s e n   θ + R   c o t g   θ cos ⁡ θ - R 2 g   c o t g 2 θ 2 u 2

Multiplicamos tudo por s e n   θ :

0 = R   s e n 2 θ + R cos 2 ⁡ θ - R 2 g   c o t g   θ cos ⁡ θ 2 u 2

0 = R - R 2 g   c o t g   θ cos ⁡ θ 2 u 2

0 = R 1 - g   c o t g   θ cos ⁡ θ 2 u 2 R

Logo, temos:

1 - g   c o t g   θ cos ⁡ θ 2 u 2 R = 0

R = 2 u 2 g   c o t g   θ cos ⁡ θ

R = 2 u 2 g t g   θ sec ⁡ θ

Resposta

R = 2 u 2 g t g   θ sec ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A partícula P se desloca ao longo da ranhura curva, uma parte desta é mostrada. Sua distância em metros medida ao longo da ranhura é dada por s = t 2 / 4 , onde t é em segundos. A partícula está em A
Uma partícula que se move em um movimento curvilíneo tem coordenadas em milímetros que variam com o tempo t em segundos de acordo com x = 3 t 2 - 4 t e y = 4 t 2 - 1 3 t 3 . Determine os módulos da ve
Com que velocidade horizontal mínima u um menino pode jogar uma pedra em A e fazê-la por pouco ultrapassar a obstrução em B ?
Se o cano da espingarda mostrada aponta para o ponto A , calcule a distância δ abaixo de A até o ponto B onde a bala incide. A velocidade de saída no disparo da bala é de 600m / s .
O vetor posição de um ponto que se move no plano x - y é dado por r = 2 3 t 3 - 3 2 t 2 i + t 4 12j onde r é expresso em metros e t é expresso em segundos. Determine o ângulo entre a velocidade v e a