Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 65
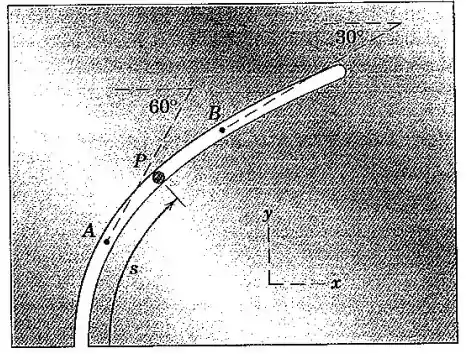
A partícula se desloca ao longo da ranhura curva, uma parte desta é mostrada. Sua distância em metros medida ao longo da ranhura é dada por , onde é em segundos. A partícula está em quando e em quando . Determine o módulo da aceleração média de entre e . Também exprima a aceleração como um vetor usando vetores unitários e .
Passo 1
Galera, como temos a expressão de em termos de , podemos derivá-la para encontrar a velocidade :
Então, temos:
Passo 2
Agora, olhando para os ângulos da figura, vemos que:
Ou seja, usando os valores de e já encontrados:
Passo 3
Já podemos então calcular o vetor :
E agora o seu módulo:
Resposta
Exercícios de Livros Relacionados
Um foguete é liberado no ponto A a partir de um avião a jato voando horizontalmente a 1000k m / h em uma altitude de 800m . Se a propulsão do foguete permanece horizontal e dá ao foguete uma aceleraçã
Um projétil é lançado a partir do ponto A com as condições iniciais mostradas na figura. Determine a distância inclinada s que posiciona o ponto B de impacto. Calcule o tempo de voo t .
Um fuzil de artilharia de longo alcance em A está apontado em um ângulo de 45 ° com a horizontal, e seu cartucho é somente capaz de transpor o pico de montanha no topo de sua trajetória. Determine o m
Um jogador de futebol americano tenta um chute de 30m passando a bola sobre a barra horizontal e entre os postes da trave. Se ele é capaz de transmitir uma velocidade u de 30m / s à bola, calcule o ân
Um pequeno avião voando horizontalmente com uma velocidade de 300k m / h em uma altitude de 120m acima de um vale remoto deixa cair um pacote de emergência médica em A . O pacote tem um paraquedas que