Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 48

A placa retangular uniforme é liberada a partir do repouso na posição mostrada. Determine o valor de x para o qual a aceleração angular é máxima, e determine a aceleração angular correspondente. Compare suas respostas com as listadas para o problema 6 / 47 .

Passo 1

Como queremos calcular a aceleração angular, vamos precisar da seguinte equação:

∑ M O = I o α

Então primeiro precisamos de uma expressão para o momento de inércia em torno do ponto O .

Precisamos do momento de inércia da placa retangular em relação ao seu centro de massa:

I c m = 1 12 b 2 + b 2 2

E agora, pelo teorema dos eixos paralelos, o momento de inércia em relação ao ponto O será:

I O = I c m + m d 2

Onde d é a distância entre o ponto O e o centro de massa:

Pelo teorema de pitágoras:

d 2 = b 4 2 + x 2

Então:

I O = I c m + m d 2

I O = 1 12 m b 2 + b 2 4 + m b 4 2 + x 2

Vamos simplificar um pouco:

I O = 1 12 m b 2 + 1 48 m b 2 + 1 16 m b 2 + m x 2

I O = m 1 6 b 2 + x 2

Passo 2

Ok, agora falta calcular a soma dos momentos em relação ao ponto O :

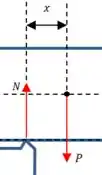
E apenas o peso P = m g vai gerar momento em relação a esse ponto:

∑ M O = I o α

m g x = 1 6 m b 2 + m x 2 α

α = g x 1 6 b 2 + x 2

E queremos encontrar o valor de x que maximiza α , ou seja, o que satisfaz d d x α = 0 :

d d x α = g 1 6 b 2 + x 2 - ( g x ) ( 2 x ) 1 6 b 2 + x 2 2 = 0

g 1 6 b 2 + x 2 - g x 2 x = 0

Agora podemos dividir por g e reorganizar a equação:

1 6 b 2 + x 2 - 2 x 2 = 0

x 2 = b 2 6

E como as soluções negativas não fazem sentido nesse caso:

x = b 6

Passo 3

E podemos calcular a aceleração angular associada a esse valor de x :

α = g x 1 6 b 2 + x 2

Substituindo x = b / 6 :

α = g b 6 b 2 6 + b 2 6

α = 6 g b 6 b 2 = g 6 b

Agora vamos comparar com as soluções que encontramos na questão 6 / 47 .

Quanto tínhamos uma barra reta de comprimento l :

x 47 = l 2 3   ;     α 47 = g 3 l

E quanto temos uma placa retangular de lados b e b / 2 :

x 48 = b 6           ;           α 48 = g 6 b

Resposta

O valor que maximiza a aceleração angular é x = b 6 . Nesse caso, a aceleração angular é α = g 6 b .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema, considerando que o impacto entre a barra AB e a superfície sem atrito é perfeitamente elástico.
16.132 Para o carro do Problema 16.131, determine a menor aceleração constante que o motorista pode manter se a porta fechar e travar, sabendo que quando a porta bate na estrutura, sua velocidade angu
Os blocos A e B têm massa de 20 kg cada, o bloco C de 14 kg e o bloco D de 16 kg. Sabendo a força para baixo de intensidade de 10 g é aplicado no bloco B, e que sistema inicia em repouso, determine em
No sistema motor mostrado na figura, l = 250m m e b = 100m m . A haste conectora B D é assumida como uma haste delgada uniforme de 1,2k g e está ligada ao pistão P de 1,8k g . Durante um teste do sist
A aceleração de uma partícula é definida pela relação a = 0,4x( 1 - k v ) , onde k é uma constante. Sabendo que em t = 0 a partícula parte o repouso em x = 4m e que, quando t = 15s ,v = 4m / s , deter