Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas de Revisão - Ex. 184

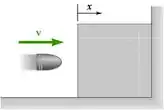
Um projétil entra em um meio resistente em x = 0 com uma velocidade inicial v0 = 270 m/s e percorre 100 mm antes de entrar em repouso. Considerando que a velocidade do projétil é definida pela relação v = v0 - kx, onde v é expressa em m/s e x é em metros, determine (a) a aceleração inicial do projétil, (b) o tempo requerido para que o projétil penetre 97,5 mm no meio resistente

Passo 1

Fala ai pessoal tudo bem? O enunciado pede que a gente determine a aceleração inicial do projétil, (b) o tempo requerido para que o projétil penetre 97,5 mm no meio resistente

Quando

x = 4 12 ft ,   v = 0 :             0 = 270   m /s - k 4 12 m

ou

k = 90   m / s

Passo 2

  1. Nós temos

    2. v = v 0 - k x

    Então

    a = d v d t = d d t v 0 - k x = - k v

    a = - k v 0 - k x

    Em t = 0:

    a = 90 1 s 270   m /s - 0 = 24300   m / s ²

    Passo 2

  2. Nós temos

d x d t = v = v 0 - k x

Em t = 0, x = 0

∫ 0 x d x v 0 - k x = ∫ 0 t d t

t = 1 k ln v 0 v 0 - k x = 1 k ln 1 1 - k v 0 x

:

t = 1 90 1 s ln 1 1 - 90 /s 270   m /s 3.9 2 m

Resposta

a )   a 0 = 24300   m / s ²

b )   t = 1.366 × 10 - 3   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A rotação da haste OA em torno de O e definida pela relação θ = (4t2 - 8t), onde θ e t são expressos em radianos e segundos, respectivamente. O cursor B desliza ao longo da haste de tal modo que sua d
Sabendo que o diâmetro do sol e de 1382 × 103 km e que a aceleração da gravidade na sua superfície e de 270 m/s2, determine o raio da orbita do planeta indicado em torno do sol considerando que a orbi
Um satélite vai percorrer indefinidamente uma orbita circular em torno de um planeta se o componente normal da aceleração do satélite for igual a g(R/r)2, onde g e a aceleração da gravidade na superfí
Sabendo que o raio da Terra e 6.370 km, determine o tempo que o telescópio espacial Hubble leva para percorrer uma orbita, considerando que o telescópio percorre uma orbita circular 590 km acima da su
Um satélite vai percorrer indefinidamente uma orbita circular em torno de um planeta se o componente normal da aceleração do satélite for igual a g(R/r)2, onde g e a aceleração da gravidade na superfí