Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 176
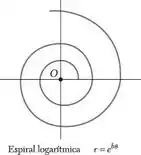
Uma partícula se move ao longo da espiral mostrada na figura. Determine a intensidade da velocidade da partícula em termos de b, , .
Passo 1
Partiu mais uma questão de resmat, tudo bem? O enunciado pede que a gente determine a intensidade da velocidade da partícula em termos de b, , . Gurizada mas não se apavorem de véspera, é uma sequência de expressões envolvendo os ângulos para determinarmos que o exercício pede, partiu :D
Temos uma Espiral logarítmica então o raio é dado por:
E a aceleração em função dos raios e angulo é dada por:
Passo 2
Como = = constante, = , escrevemos:
Resposta
Exercícios de Livros Relacionados
41. Uma partícula está se movendo ao longo de uma linha reta de maneira que sua posição de um ponto fixo é s = 12 - 15 t 2 + 5 t 3m , onde t é dado em segundos. Determine a distancia total percorrida
26. A aceleração de uma partícula movendo-se ao longo de uma linha reta é a=0,02etms2, onde t é dado em segundos. Se v=0, s=0 quando t=0, determine a velocidade e a aceleração da partícula em s=4m.
32. A bola A é jogada verticalmente para cima do topo de um prédio de 30m com uma velocidade inicial de 5 m/s. No mesmo instante, outra bola B é jogada para cima a partir do chão com uma velocidade in
36. A aceleração de uma partícula movendo-se ao longo de uma linha reta é a = 8 - 2 sm / s 2 , onde s é dado em metros. Se v = 0e ms = 0 , determine a velocidade da partícula em s = 2m e a posição da
27. Uma partícula move-se ao longo de uma linha reta com uma aceleração de a = 5 3 s 1 3 + s 5 2m / s 2 , onde sé é dado em metros. Determine a velocidade da partícula quando s = 2m, se ela partir do