Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 44

Usando o método da Sec. 7.4, resolver o Prob. 7.14

Passo 1

Pessoal essa questão pede para fazermos o diagrama do momento fletor e da força cortante para a viga representada. A primeira coisa que temos de fazer é achar as forças de reação em e em .

Depois o que vamos fazer é realizar diversos cortes na viga e achar as forças cortantes. Aí depois para achar o momento fletor vamos integrar a equação da força cortante:

Passo 2

Vamos começar calculando as reações:

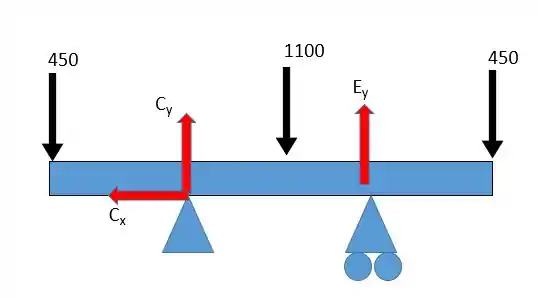
Como só existe uma força em essa força é nula, portanto . Agora podemos aplicar as equações da estática:

Agora o momento aplicado no ponto e considerando o sentido horário positivo:

Dessa forma:

Passo 3

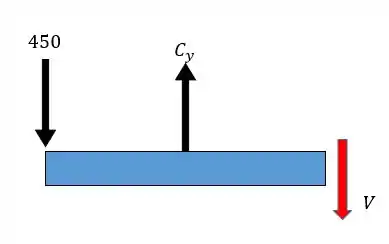
Agora vamos achar a força cortante. Galera aqui vai uma dica para fazermos isso de forma mais rápida e prática, quando temos apenas forças pontuais então a força cortante será igual à soma de todas as forças que estão antes do ponto que estamos analisando, veja:

Para o trecho

Para o trecho :

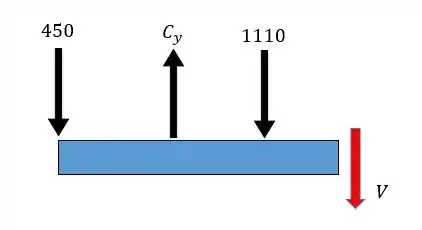
Para o trecho :

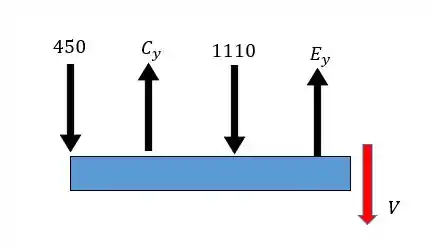
Para o trecho :

Temos portanto:

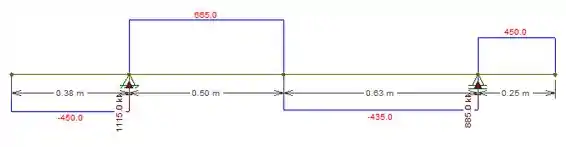
Podemos ver que o maior valor absoluto é:

Passo 4

Agora vamos partir para o momento fletor a gente não precisa fazer as seções novamente só precisamos integrar os valores:

Para o trecho :

Logo,

Para o trecho :

Logo,

Para o trecho :

Logo,

Para o trecho :

Logo,

Representando num diagrama:

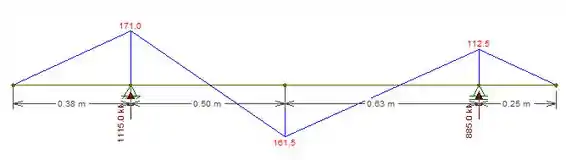
Podemos ver que o maior valor absoluto é quando :

Resposta

a)

b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar a largura b da viga e a distância x , para que a tensão normal máxima σ m e a tensão máxima de cisalhamento τ m na viga sejam simultaneamento iguais

Para a viga com o carregamento mostrado, determinar a largura b da viga e a distância x , para que a tensão normal máxima σ m e a tensão máxima de cisalhamento τ m na viga sejam simultaneamento iguais

Usando a equação derivada da parte b do Prob. 7.126, mostrar que, em qualquer seção transversal da viga da Fig. 7.24, onde x ≥ 0,5444c , o maior valor de σ m á x á ocorre para y = c . (Sugestão: Denot

A barra de 100m m de largura suporta uma carga de 11k N e repousa sobre uma fundação, que exerce um carregamento linearmente distribuído como mostrado. Pde-se: (a) Determinar os valores de w A e w b ,

Duas placas de cobertura, cada uma com 12,7m m de espessura, são soldadas a uma viga de perfil W 530 × 92 , como mostrado. Sabendo-se que l = 4,2 m e b = 250m m , determinar a máxima tensão normal em