Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 151

No projeto desse mecanismo, o movimento da placa quadrada é controlado pelas duas barras articuladas. A barra AO possui uma velocidade angular constante ω = 4 r a d / s durante um curto intervalo de movimento. Para o instante representado, θ = tan - 1 ⁡ 4 / 3   e o lado AB está paralelo ao eixo x. Para esse instante, determine a aceleração angular da placa e da barra CB.

Passo 1

Galera, como já é de costume, primeiro vamos organizar todos os dados do enunciado e fazer um esboço do que realmente importa no mecanismo.

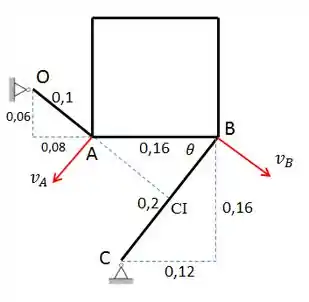
Vamos começar calculando as velocidades de A e B. Pela barra AO, calculamos o módulo da velocidade de A:

v A = ω × r = 4 × 0,1 = 0,4   m / s

Pela figura, vemos que CI é o Centro Instantâneo da placa AB. Então, calculamos a velocidade angular da placa:

ω A B = v A r A / C I = 0,4 0,16 ( 4 5 ) = 3,125 r a d s

E a velocidade de B:

v B = ω A B × r B / C I = 3,125 × 0,1 6 ( 3 5 ) = 0,3   m / s

ω B C = v B r B / C = 0,3 0,2 = 1,5 r a d s

Bom, agora vamos começar a calcular as acelerações. Pela barra AO, podemos calcular a aceleração de A:

a A = - r A O ω A O 2 + α A O × r A O = - 4 2 ( 0,0 8 i ^ - 0,06 j ^ ) + 0

a A = - 1,28 i ^ + 0,96 j ^   m / s 2

Agora, fazemos o mesmo para achar a aceleração de B em relação à barra BC:

a B = - r B C ω B C 2 + α B C × r B C = - 1,5 2 ( 0,12 i ^ + 0,16 j ^ ) + α B C ( - 0,16 i ^ + 0,1 2 j ^ )

a B = - 0,27 i ^ - 0,36 j ^ + α B C ( - 0,16 i ^ + 0,12 j ^ )

Passo 2

Neste passo, vamos usar a equação da aceleração relativa para os pontos A e B.

a B = a A + a B / A n + a B / A t

Onde:

a B / A n = ω A B × ω A B × r B / A = - 3,125 2 0,16 i ^ = - 1,5625 i ^   m / s 2

a B / A t = α A B × r B / A = α A B 0,16 j ^ m / s 2

Agora, vamos substituir os valores encontrados na equação da aceleração relativa:

- 0,27 i ^ - 0,36 j ^ + α B C - 0,16 i ^ + 0,12 j ^ = - 1,28 i ^ + 0,96 j ^ - 1,5625 i ^ + α A B 0,16 j ^  

Decompondo nas direções, temos o sistema:

- 0,27 i ^ + α B C - 0,16 i ^ = - 1,28 i ^ - 1,5625 i ^

- 0,36 j ^ + α B C + 0,12 j ^ = + 0,96 j ^ + α A B 0,16 j ^

Resolvendo o sistema, temos:

α B C = 16,08   k ^   r a d / s 2

α A B = 3,81 k ^   r a d / s 2

Resposta

α B C = 16,08   k ^ r a d s 2

α A B = 3,81 k ^ r a d s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pino P desliza em uma ranhura circular cortada na placa mostrada na figura com uma velocidade relativa constante u = 90m m / s . Sabendo que, no instante mostrado, a velocidade angular ω da placa é
No instante mostrado na figura, a barra BC tem uma velocidade angular de 3r a d / s e uma aceleração de 2r a d / s 2 , ambas no sentido horário. Determine a aceleração angular da placa.
Sabendo que, no instante mostrado na figura, a barra articulada em B gira no sentido anti-horário com velocidade angular constante ω B de 6 rad /s, determine a velocidade angular e a aceleração angula
No instante mostrado na figura, a barra BC tem uma velocidade angular de 3r a d / s e uma aceleração de 2r a d / s 2 , ambas no sentido horário. Determine a aceleração angular da placa.
No Problema 15.179, determine a velocidade e a aceleração angulares do disco S no instante em que ϕ = 135 °