Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 148

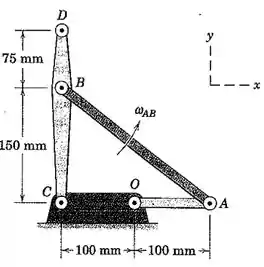
Se a barra AB do mecanismo de quatro barras possui uma velocidade angular constante no sentido anti-horário de 40 rad/s durante um intervalo que inclui o instante representado, determine a aceleração angular de AO e a aceleração do ponto D. Expresse seus resultados em notação vetorial.

Passo 1

Galera, como já é de costume, primeiro vamos organizar todos os dados do enunciado e fazer um esboço do mecanismo.

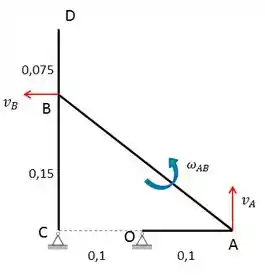
Vamos começar calculando as velocidades de A e B. Pela Figura, vemos que o ponto C é o Centro Instantâneo de Velocidade nula. Portanto:

v A = ω A B × r A C = 40 k ^ × 0,2 i ^ = 8 j ^ m s

v B = ω A B × r B C = 40 k ^ × 0 , 15 j ^ = - 6 i ^ m s

Com esses valores, calculamos as velocidades angulares das barras AO e BC:

ω A O = v A r A O = 8 0,1 = 8 0 k ^ m s

ω B C = v B r B C = 6 0 , 15 = 4 0 k ^ m s

Agora, podemos começar a calcular as acelerações.

Vamos fazer primeiro para as barras articuladas fixas em um ponto. A partir da barra AO:

a A = - r A O ω A O 2 + α A O × r A O = - 80 2 0 , 1 i ^ + 0,1 α A O j ^

a A = - 640 i ^ + 0,1 α A O j ^   m / s 2

Da mesma forma, fazemos para a barra BC:

a B = - r B C ω B C 2 + α B C × r B C = - 40 2 0,1 5 j ^ - 0,1 5 α B C i ^

a B = - 240 j ^ - 0,1 5 α B C i ^   m / s 2

Passo 2

Neste passo, vamos usar a equação da aceleração relativa para os pontos A e B.

a B = a A + a B / A n + a B / A t

Onde:

a B / A n = ω A B × ω A B × r B / A = - 40 2 - 0,2 i ^ + 0,15 j ^ = 320 i ^ - 240 j ^   m / s 2

a B / A t = α A B × r B / A = 0 ,   p o i s   ω A B = c n t e

Agora, vamos substituir os valores encontrados na equação da aceleração relativa:

- 240 j ^ - 0,15 α B C i ^ = - 640 i ^ + 0,1 α A O j ^ + 320 i ^ - 240 j ^  

Decompondo nas direções, temos o sistema:

- 0,15 α B C i ^ = - 640 i ^ + 320 i ^

- 240 j ^ = + 0,1 α A O j ^ - 240 j ^  

Resolvendo o sistema, temos:

α A O = 0   k ^   r a d / s 2

α B C = α D C = 2133,33   k ^   r a d / s 2

E, por fim, para encontrar a aceleração de D:

a D = - r D C ω D C 2 + α D C × r D C = - 40 2 0 , 22 5 j ^ - 0,22 5 ( 2133,33 )   i ^

a D = - 480 i ^ - 360 j ^   m / s 2

Resposta

α A O = 0   k ^   r a d / s 2

a D = - 480 i ^ - 360 j ^   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 90 ∘ , determine a aceleração (a) do colar D, (b) do ponto médio G da barra BD.
O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 60 ∘ , determine a aceleração do colar D,
Sabendo que, no instante mostrado, a haste AB tem aceleração angular zero e uma velocidade angular de 15 rad/s no sentido anti-horário, determine (a) a aceleração angular do membro BD, (b) a aceleraçã
A gaiola de um elevador de mina se move para baixo a uma velocidade constante de 40 pés / s. Determine a magnitude e a direção da aceleração de Coriolis da gaiola se o elevador estiver localizado (a)
O corpo AB e a haste BC do componente robótico mostrado giram a uma taxa constante ω 1 = 0.60 r a d / s em torno do eixo Y. Simultaneamente, um controle de arame e polia faz com que o braço CD gire em