Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 86
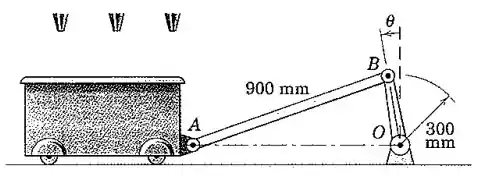
No projeto de uma planta de processamento de produção, uma cuba móvel com produtos está oscilando sob água pulverizada através da ação da barra de conexão AB da manivela OB. Para o instante em que , a velocidade angular de AB é de 0,086 rad/s no sentido anti-horário. Encontre a velocidade angular correspondente a e a velocidade da cuba. Resolva a equação da velocidade relativa pela álgebra vetorial ou pela geometria de vetores.
Passo 1
Olhando para a Figura do enunciado, fica evidente o triangulo AOB, que pode ajudar para resolver a questão por geometria. Temos ainda como dados dois lados e um ângulo do triângulo, além da velocidade angular de AB.
Para resolver o problema por geometria dos vetores, é preciso analisar os vetores velocidades dos principais pontos, que neste caso é a barra AB.
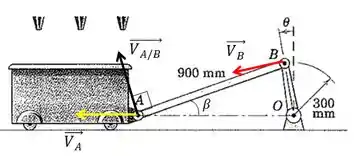
O ponto B, por estar em uma barra articulada em O, possui velocidade perpendicular ao segmento , e pode ser calculada por:
Já o ponto A, que se encontra no carrinho, irá de deslocar apenas na direção horizontal para esquerda (pois a velocidade angular gira no sentido anti-horário). Vale lembrar que o vetor velocidade relativa possui direção perpendicular à barra AB, e pode ser calculada por:
Passo 2
Analisando o triângulo AOB e o BOD, podemos usar relações geométricas encontrar o ângulo
x
x
Temos duas formas de encontrar o x indicado na Figura:
Passo 3
Nesta etapa, iremos unir os vetores velocidade para resolver a equação da velocidade relativa.
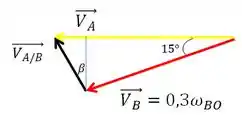
Agora, basta aplicar a Lei dos senos no triângulo acima para descobrir a velocidade angular :
E, finalmente, usamos o triângulo para determinar a velocidade do ponto A:
)
para a esquerda