Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas de Revisão - Ex. 154
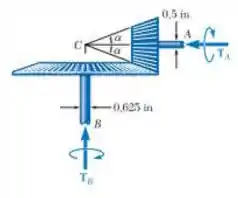
No sistema de engrenagens cônicas mostrado, . Sabendo que a tensão de cisalhamento admissível é de 8 ksi em cada eixo e que o sistema está em equilíbrio, determine o maior torque de que pode ser aplicado em A.
Passo 1
Fala aí rapaziada tudo certo? O enunciado pede que a gente determine o maior torque de que pode ser aplicado em A. Então usando limite de tensão para o eixo A, temos:
Usando limite de tensão para o eixo B,
Considerando
O valor permitido de é o menor.
Resposta
Exercícios de Livros Relacionados
O eixo da hélice do hidrofólio é de aço A-36 e tem 30m de comprimento. Está acoplado a um motor diesel em linha, o qual transmite uma potência máxima de 2.000k W e provoca rotação de 1.700r p m no eix
O parafuso de aço A-36 com 8 mm de diâmetro está parafusado firmemente ao bloco em A. Determine as forças conjugadas F que devem ser aplicadas à chave de torque de modo que a tensão de cisalhamento má
O eixo de aço A-36 é composto pelos tubos A B e C D e uma seção maciça B C . Está apoiado em mancais lisos que permitem que ele gire livremente. Se as engrenagens, presas às extremidades do eixo, fore
O eixo de aço A-36 de 20m m de diâmetro é submetido aos torques mostrados. Determine o ângulo de torção da extremidade B .
A haste de latão com 0,8 in. de diâmetro de 30 in. de comprimento é girada em um ângulo de 10°. Utilizando o diagrama τ - γ mostrado para a haste de latão dada, determine (a) a intensidade do toRque a