Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 85
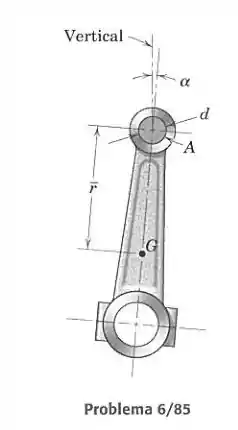
No projeto de um teste de atrito, o eixo é frouxamente preso ao mancal da biela, que tem centro de gravidade em , como mostrado. Com a biela inicialmente na posição vertical, o eixo é girado lentamente até que a biela escorregue em um ângulo . Escreva uma expressão exata para o coeficiente de atrito .
Passo 1
O eixo deve aplicar sobre o mancal uma resultante , composta pelo atrito e pela força normal. Essa resultante deve fazer com a normal à superfície de contato o ângulo de atrito , que possui relação com o coeficiente de atrito dado pela fórmula:
Pelo equilíbrio do eixo, essa força deve ser para cima,para suportar seu peso. Vamos representar então a força peso e :
Passo 2
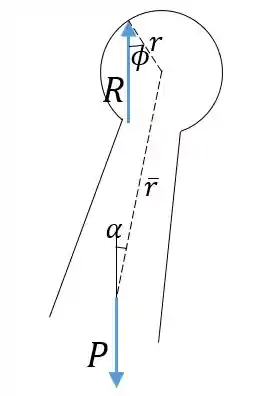
No limiar do movimento, ainda há equilíbrio, então as duas forças são iguais e o momento em torno do centro do eixo deve ser zero. A distância da linha de ação de até o centro é e a distância horizontal entre e centro do eixo é . Então:
Como as forças são iguais, cortamos as duas:
Então obtemos o seno do ângulo de atrito:
Passo 3
Como , vamos achar a tangente através do seno. Pela relação fundamental trigonométrica:
Então:
Dividindo em cima e em baixo por :