Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 140

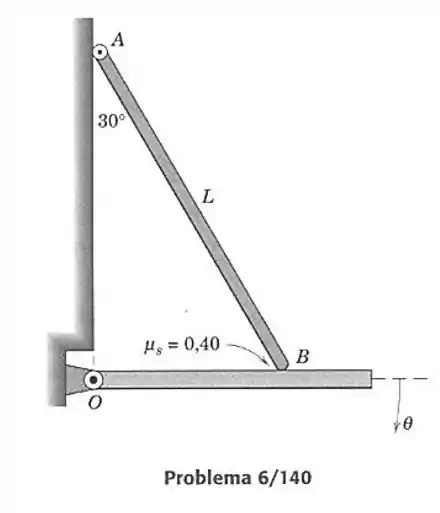
140- O pequeno rolamento na extremidade superior da barra uniforme está apoiado contra a superfície vertical em A , enquanto a extremidade arredondada B repousa sobre a plataforma que está ligeiramente girada para baixo a partir da posição horizontal mostrada. Para um coeficiente de atrito estático μ s = 0.40 em B , determine o ângulo θ da plataforma no qual ocorrerá deslizamento. Despreze o tamanho e o atrito do rolamento e a pequena espessura da plataforma.

Passo 1

Para fazer essa questão vamos desenhar o diagrama de forças e considerar que a plataforma onde a barra se apoia está ligeiramente inclinada tal como está escrito no enunciado.

Para um comprimento da barra A B igual a L podemos dizer pelo ângulo de 30 que o comprimento de O B vale:

sin ⁡ 30 = O B L → O B = L 2

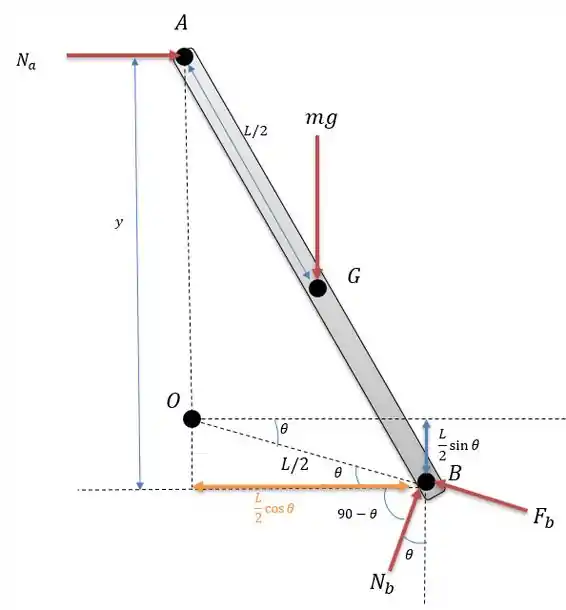
Pela figura o valor de y valerá:

L 2 = y 2 + L 2 cos ⁡ θ 2

y = L 2 - L 2 4 cos 2 ⁡ θ = L 2 4 - cos 2 ⁡ θ = L 2 4 - c o s 2 θ

Logo O A valerá:

O A = L 2 4 - c o s 2 θ - L 2 sin ⁡ θ = L 2 ( 4 - cos 2 ⁡ θ - sin ⁡ θ )  

Passo 2

Podemos calcular o valor de F b pelo coeficiente de atrito que a mesma faz com o chão:

F b = 0.4 N b

Fazendo a somatória das forças verticais nós teremos:

- m g + N b cos ⁡ θ + 0.4 N b sin ⁡ θ = 0

Agora fazendo a somatória das forças horizontais:

N a - ( 0.4 N b cos ⁡ θ ) + N b sin ⁡ θ = 0

Fazendo a somatória dos momentos em O (considerando o sentido horário como positivo) temos:

N a × L 2 ( 4 - cos 2 ⁡ θ - sin ⁡ θ )   - N b L 2 + m g L c o s   θ 4 = 0

A força de atrito não gera momento em O .

Passo 3

Pela primeira equação nós encontramos:

N b cos ⁡ θ + 0.4 N b sin ⁡ θ = m g → N b = m g cos ⁡ θ + 0.4 sin ⁡ θ

Substituindo esse valor na segunda equação nós encontraremos:

N a = N b ( 0.4 cos ⁡ θ - sin ⁡ θ ) = m g × 0.4 cos ⁡ θ - sin ⁡ θ 0.4 sin ⁡ θ + cos ⁡ θ

Colocando esses valores na equação do momento vemos que ela assuimirá valor de 0 somente quando θ = 5.8   °  

Com valores menores que 5.8 ° a força de atrito consegue se ajustar a ponto de fazer com que o sólido fique no lugar, maiores que isso não.

Resposta

θ = 5.8 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco retangular homogêneo de massa m repousa sobre o plano inclinado que é articulado em torno de um eixo horizontal através de O . Se o coeficiente de atrito estático entre o bloco e o plano for μ
A placa semicircular de 5k g gira em torno de um rolamento fixo em O que pode exercer um momento de atrito máximo de 1,2N m na placa. A força horizontal P é aplicada a uma corda enrolada em torno da p
Determine o coeficiente de atrito estático mínimo entre a bobina uniforme de 50 kg e a parede de modo que ela não deslize.
Determine a força P máxima que pode ser aplicada sem causar o movimento da caixa de 100 kg com centro de gravidade em G . O coeficiente de atrito estático no piso é μ s = 0 , 4 .
Determine a força P máxima que pode ser aplicada sem causar o movimento das duas caixas de 50 kg. O coeficiente de atrito estático entre cada caixa e o piso é μ s = 0,25 .