Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 70

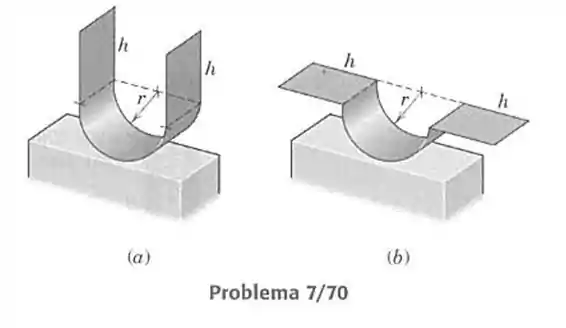
70- Duas cascas semicilíndricas com retângulos projetados iguais são formadas de lâminas metálicas, uma com a configuração a ) e a outra com configuração b ) . Ambas as cascas repousam sobre uma superfície horizontal. Para o caso a ) determine o valor máximo de h para o qual a casca se manterá estável na posição mostrada. Para o caso b ) prove que a estabilidade na posição mostrada não é afetada pela dimensão h .

Passo 1

Sabendo que o centroide de um circulo é igual a G = 2 r π com medida começando pelo seu centro e que a densidade linear dos sólidos são iguais a suas densidades de área nós temos a seguinte representação para a letra a ) se dermos uma entortada em θ na figura.

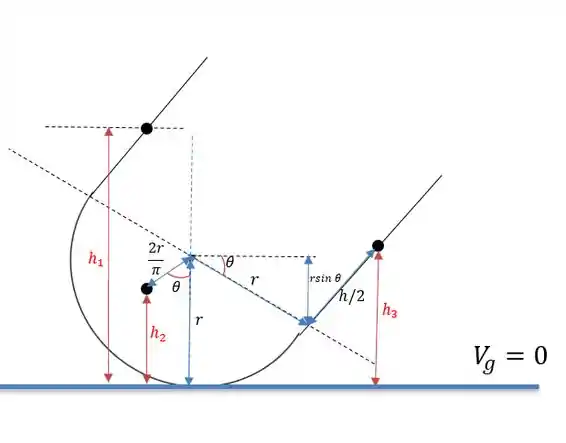
Onde temos a presença de três corpos, as duas barras delgadas de comprimento h e a semicircunferência de raio r .

A altura vertical do centro de massa da semicircunferência tem altura h 2 e vale:

h 2 = r - 2 r π cos ⁡ θ

Onde precisaremos rebater seu centro de massa na vertical para sabermos sua referência em relação ao eixo nulo de energia potencial gravitacional.

A barra mais a direita e tem altura h 3   e sua altura em relação ao eixo nulo de energia potencial vale:

h 3 = r - r s i n   θ + h 2 cos ⁡ θ

Já a altura h 1 valerá:

h 1 = r + r s i n   θ + h 2 cos ⁡ θ

Portanto a energia potencial do sistema todo valerá:

V g = m s g r - 2 r π cos ⁡ θ + m h g r - r s i n   θ + h 2 cos ⁡ θ + m h g r + r s i n   θ + h 2 cos ⁡ θ

Onde m s é a massa da semicircunferência e m h a massa da barra de comprimento h .

Passo 2

Porém não podemos escrever a energia do sistema com essas massas, para isso sabemos que o corpo é feito de um mesmo material de densidade igual a ρ e que a mesma tem fórmula igual a:

ρ = m L

Onde L é o comprimento da linha. Dessa forma:

m s = ρ L s = ρ π r

Onde π r é o comprimento da semicircunferência.

E

m h = ρ L h = ρ h

Logo a energia total do sistema valerá:

V = ρ π g r 2 - 2 r 2 π cos ⁡ θ + ρ g h 2 r + h cos ⁡ θ

Derivando essa equação em relação a θ nós teremos:

d V d θ = 2 ρ g r 2 sin ⁡ θ - ρ g h 2 sin ⁡ θ

Igualando essa expressão a zero nós encontraremos as posições de equilíbrio.

θ = 0

2 r 2 - h 2 = 0

2 r 2 = h 2

h = r 2

Isso já prova uma dependência de h para se ter um equilíbrio do sistema.

Derivando pela segunda vez em relação a θ , nós teremos a seguinte equação para a estabilidade.

d 2 V d θ 2 = 2 ρ π g r 2 cos ⁡ θ - ρ g h 2 cos ⁡ θ > 0

Considerando qualquer valor de θ para adquirirmos a estabilidade temos que:

2 ρ π g r 2 > ρ g h 2

2 r 2 > h 2

h < r 2

Então o maior valor para o qual h pode ser para o sistema ser estável é h = r 2

Passo 3

Letra b) Para esse sistema nós teremos a seguinte representação abaixo.

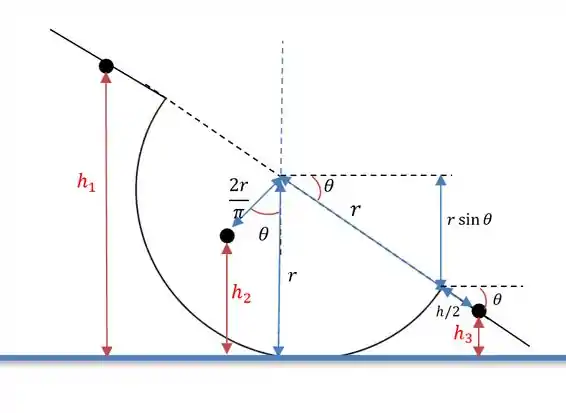
A altura h 2 continua sendo r - 2 r π cos ⁡ θ o que muda agora são as alturas h 1 e h 3 . Com os ângulos de θ temos que:

h 3 = r - r s i n   θ - h 2 sin ⁡ θ  

E

h 1 = r + r s i n   θ + h 2 sin ⁡ θ

Com os valores de m s e m h temos uma equação de energia igual a:

V = ρ π r 2 - 2 r 2 π cos ⁡ θ + ρ h r - r s i n   θ - h 2 sin ⁡ θ + ρ h ( r + r s i n   θ + h 2 sin ⁡ θ )

V = ρ π r 2 - 2 r 2 π cos ⁡ θ + 2 ρ h r

Derivando essa equação de energia em relação a θ teremos:

d V d θ = 2 ρ r 2 sin ⁡ θ

E como temos a variável h para equação do equilíbrio também não iremos ter para a estabilidade, logo não temos dependência de h .

Resposta

Letra a) h = r 2

Letra b) d V d θ = 2 ρ r 2 sin ⁡ θ   equação independente de h .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um binário M de intensidade 100N ⋅ M é aplicado, tal como mostra a figura, à manivela de um sistema motor. Sabendo que A B = 50m m e B C = 200m m , determine a força P necessária para se manter o equi
Determine o valor de θ correspondente para a posição de equilíbrio do mecanismo do problema 10.11, quando P = 200N e Q = 720N .
Determine o valor de θ correspondente para a posição de equilíbrio do mecanismo do problema 10.9, quando P = 80N e Q = 100N .
A barra AB é fixada ao bloco A que desliza sem atrito na fenda vertical como mostrada na figura. Desprezando o efeito do atrito e o peso das barras, determine o valor de θ correspondente ao equilíbrio
Resolva o problema da 10.25 considerando que a força de 800N é substituída por um binário de 24N ⋅ m no sentido horário aplicado em D.