Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 74
Prove que o avanço deverá ser menor que para que o parafuso mostrado na Figura seja “autotravante”.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Temos o seguinte diagrama da figura :
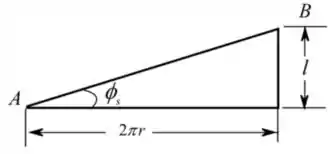
Sabemos que o ângulo de fricção é dado por:
Para o autotravamento, o ângulo de atrito estático deve ser maior que o ângulo de ataque.
Para que isso ocorra, temos que:
Substituindo as equações, temos que:
Portanto:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Se cada caixa pesa 75k g , determine a menor força horizontal P que o homem precisa exercer na caixa de cima a fim de causar movimento. O coeficiente de atrito estático entre as caixas é μ s = 0,5 , e
O carpinteiro empurra lentamente a tábua uniforme horizontalmente sobre o topo do cavalete. A tábua tem um peso uniforme de 50N / m , e o cavalete tem um peso de 75N e centro de gravidade em G . Deter
O carpinteiro empurra lentamente a tábua uniforme horizontalmente sobre o topo do cavalete. A tábua tem um peso uniforme de 50N / m , e o cavalete tem um peso de 75N e centro de gravidade em G . Deter
Se cada caixa pesa 75k g , determine a menor força horizontal P que o homem precisa exercer na caixa de cima a fim de causar movimento. O coeficiente de atrito estático entre as caixas é μ s = 0 , 6 5
Se a garota com 35k g estiver na posição d = 1,2m , determine o coeficiente mínimo de atrito estático μ s nos pontos de contato A e B de modo que a tábua não deslize. Despreze o peso da tábua.