Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 62
62. Resolva o Problema 9.13 usando o círculo de Mohr.
Passo 1
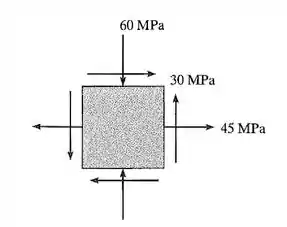
(a) Da seguinte figura de estado plano, tiramos que:
Passo 2
Como estamos trabalhando com Círculo de Mohr, a primeira coisa a se fazer é determinar o centro do círculo, que é dado por:
Substituindo os valores numéricos correspondentes, chega-se à:
E em seguida, vamos determinar o raio do nosso círculo, através da fórmula da tensão de cisalhamento máximo:
Trocamos as variáveis pelos seus respectivos valores numéricos:
Lembremos então, da fórmula das tensões principais, onde obtemos duas tensões, uma máxima e uma mínima
E como temos o valor de e de , obtemos então, que:
Com isso, já podemos fazer o esboço do nosso círculo:
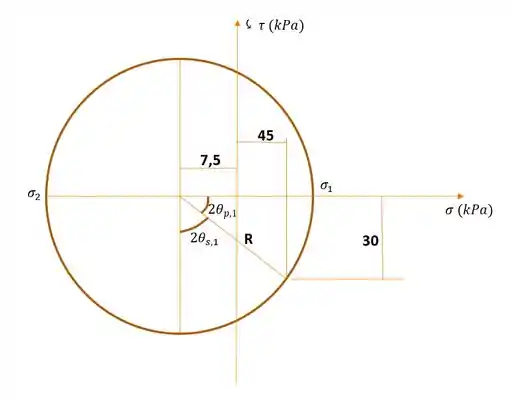
Agora, falta apenas determinar o ângulo em que o nosso elemento está orientado. Ora bolas, se você olhar para o círculo, verá que o nosso ângulo, que chamaremos de , é dado por:
Como o primeiro ângulo é igual a , tiramos que:
Passo 3
(b) Bom! Essa letra pede pra gente determinar a tensão máxima de cisalhamento, a tensão média e a orientação do elemento cisalhante.
Mas, olha só já temos a resposta de ao menos dois itens. Afinal a tensão máxima de cisalhamento é o raio do nosso círculo de Mohr e a tensão média é o centro do nosso círculo. Logo, obtemos que:
Falta agora, a orientação do nosso elemento cisalhante! Por isso voltemos ao círculo de Mohr.
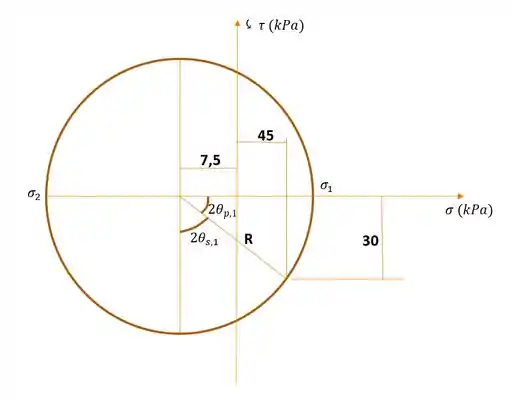
Olhando essa figura, percebemos que o nosso ânngulo cisalhante que é um ângulo complementar a , é dado por:
Como o primeiro ângulo é igual a , tiramos que:
No caso do ângulo cisalhante, se o valor deu positivo é porque o sentido dessa vez é horário. Duvida? Basta lembrar da fórmula para encontrar :
Como na circunferência, trabalhamos com distância absoluta o da fórmula foi omitido. Por isso, se deu positivo, nesse caso o sentido é horário.
Resposta
(a)
(b)