Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 69

Um quadrado de 1in, foi riscado na lateral de um grande vaso de pressão. Depois de pressurizado é mostrada a condição de tensão biaxial no quadrado. Sabendo que E = 29   x   10 6   p s i     e     v = 0,30 , determine a mudança de comprimento do (a) lado AB, (b) lado BC, (c) da diagonal AC.

Passo 1

E ai gurizada tudo belezinha? Para determinarmos a mudança de comprimento do dos lados AB, BC e AC do elemento apresentado, antes precisamos determinar a deformação que ocorre em X e em Z, vamos lá !!

ε x = 1 E σ x - v σ y = 1 29   x   10 6 12   x   10 3 - 0,30   x   6   x   10 3 = 351,72     x   10 - 6 ε z = 1 E σ y - v δ z = 1 29   x   10 6 6   x   10 3 -   0,30   x ( 12   x   10 3 ) = 82,759   x   10 - 6

Agora sim gurizada vamos determinar as mudanças destes comprimentos

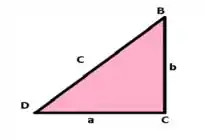
  1. δ A B = ( A B ) 0 ε x = 1,00   x   351,72   x   10 - 6 = 352   x   10 - 6 i n .
  2. δ B C = ( B C ) 0 ε y = 1,00   x   82,759   x   10 - 6 = 82,8   x   10 - 6 i n .  

    3. Agora para determinarmos em AC notem que teremos um triangulo, como exposto abaixo, teremos que usar Pitágoras, partiu!!

  3. A C = A B 2 + B C 2 = A B 0 + δ x 2 + B C 0 + δ y 2 = 1 + 351,72   x   10 - 6 2 + 1 + 82,759   x   10 - 6 2 = 1,41452 ( A C ) 0 = 2             A C - ( A C ) 0 = 307   x   10 6   i n

Resposta

  1. 351,72     x   10 - 6 i n
  2. 82,759   x   10 - 6 i n
  3. 307   x   10 6   i n
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para um elemento sob carga axial, expresse a deformação normal ϵ ' em uma direção que forma um ângulo de 45° com o eixo de carga em função da deformação axial ϵ fazendo (a) a comparação da hipotenusa
Qual a força de P que deverá ser aplicada à placa do problema 2.75 para produzir um deslocamento de 1 16 i n ?
Uma barra de latão AB é envolvida por uma jaqueta utilizada para aplicar uma pressão hidrostática é 40M P a na parte BC de 240 - m m da barra. Sabendo que E = 105G P a e v = 0,33 , determine (a) a var
O bloco mostrado na figura é feito de liga de magnésio com E = 34G P aev = 0,35 . Sabendo que σ x = - 180M P a , determine (a) a intensidade de σ x para qual a qual a variação na altura do bloco será
A placa homogênea ABCD está submetida a um carregamento biaxial como mostra a figura. Sabe-se que σ z = σ 0 e que a variação o comprimento da placa na direção x deve ser zero, ou seja, ϵ x = 0 . Desig