Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 55

Duas barras de aço ( E a ç o = 200   G P a     e     a a ç o = 11,7   x   10 - 6 / ° C ) são utilizadas para reforçar uma barra de latão ( E l a t ã o = 105   G P a ,   a l a t ã o = 20,9   x   10 - 6 / ° C ) que está submetida a uma força P = 25   k N . Quando as barras de aço foram fabricadas, a distância entre os centros dos furos que deveriam encaixar os pinos foi feita 0,5 mm menor do que os 2 m necessários. As barras de aço foram então colocadas em um forno para aumentar seu comprimento para que pudessem encaixar-se nos pinos. Após a fabricação, a temperatura das barras de aço voltou a ser temperatura ambiente. Determine (a) o aumento na temperatura necessário para que as barras de aço se encaixassem nos pinos e (b) a tensão na barra de latão depois que a força foi aplicada a ela.

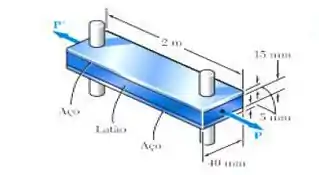
Passo 1

Fala aí galera tudo belezinha? Para calcularmos o aumento na temperatura, vamos determinar o alongamento da seção...

  1. Mudanças de temperatura necessárias para fabricação.

    2. δ T = 0,5   m m = 0,5   x   10 - 3 m

    Mudança de temperatura necessária para expandir a barra de aço por esse valor.

    δ T = L α s ∆ T ,       0,5   x   10 - 3 = 2,00   x   11,7   x   10 - 6   x   ∆ T , ∆ T = 0,5   x   10 - 3 = 2   x   11,7   x   10 - 6   x   ( ∆ T ) ∆ T = 21 ,   368   ° C

    Passo 2

  2. Uma vez montada, uma força de tração P * se desenvolve no aço e uma força de compressão P * se desenvolve no aço latão, afim de alongar o aço e contrair o latão.

Alongamento de aço: A s = 2   x   5   x   40 = 400 m m 2 = 400     x   10 - 6 m 2 ( δ P ) s = F * L A s E s = P * ( 2,00 ) 400   x   10 - 6   x   ( 200   x   10 9 ) = 25   x   10 - 9 P *

Contração do latão: A b = 4 o   x   15 = 600 m m 2 = 600     x   10 - 6 m 2 ( δ P ) b = P * L A b E b = P * ( 2,00 ) 600   x   10 - 6   x   ( 105   x   10 9 ) = 31,746   x   10 - 9 P *

Considerando:

( δ P ) s + ( δ P ) b ,

Podemos determinar a força P:

( δ P ) s + ( δ P ) b = 0,5   x   10 - 3 ,     56,746   x   10 - 9 P * = 0,5   x   10 - 3

P *   = 8,8112   x   10 3 N

Tensões devido a fabricação:

Aço: σ * = P * A = 8,8112   x   10 3 400   x   10 - 6 = 22,028   M P a

Latão: σ b * = P * A b = 8,8112   x   10 3 600   x   10 - 6 = - 14,685   M P a

A essas tensões devem ser adicionadas as tensões devido à carga de 25 - k N

Para a carga adicionada, a deformação adicional é a mesma para o aço e o latão. Seja δ ' o deslocamento adicional. Além disso, sejam P s   e   P b as forças adicionais desenvolvidas no aço e no latão, respectivamente.

δ ' =   P L A E =   P b L A b E b P a =   A s E s L   δ ' = 400   x   10 - 6   x   200   x   10 9 2,00 δ ' = 40   x   10 6 δ ' P b =   A b E b L   δ ' = 600   x   10 - 6   x   105   x   10 9 2,00 δ ' = 31,5   x   10 6 δ '

Total:

P = P a + P b = 2,5   x   10 6 δ ' 40   x   10 6 δ ' + 31,5   x   10 6 δ ' = 25   x   10 3           δ ' = 349,65   x   10 - 6 m   P a = 40   x   10 6   x   349,65   x   10 - 6 = 13,9860   x   10 3 N P b = 31,5   x   10 6   x   394,65   x   10 - 6 = 11,0140   x   10 3 N

Determinando as tensões dos materiais temos: σ a = P A = 13,9860   x   10 3   400   x   10 - 6 = 34,965   x   10 6 P a σ l = P b A b = 11,0140   x   10 3 600   x   10 - 6 = 18,3566   x   10 6 P a

Tensões totais:

σ a = 34,965   x   10 6 + 22,028   x   10 6 = 56,991   x   10 6 P a σ l = 18,3566   x   10 6 - 14,6853   x   10 6 = 3,6713   x   10 6 P a

Resposta

  1. 21 , 38 ° C
  2. σ a = 57,0   M P a

σ l = 3,67   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco cilíndrico E de tem uma velocidade horizontal v 0 = 16f t / s quando atinge diretamente o batente BD que está conectado às hastes AB e CD com diâmetro de 1 8 _ = i n . Sabendo que as hastes sã
O anel D de 35kg é abandonado do repouso na posição mostrada e é parando por uma placa conectada na extremidade em C da haste vertical ABC. Sabendo que E=200 GPa para ambas as porções da haste, determ
O anel D de 15kg é abandonado do repouso na posição mostrada e é parando por uma placa conectada na extremidade em C da haste vertical ABC. Sabendo que E=200 GPa para ambas as porções da haste, determ
O anel G de 48 kg é liberado do repouso na posição mostrada e é parado por uma placa conectada na extremidade em C da haste vertical ABC. Sabendo que E = 200 GPa para ambas as porções da haste, determ
O bloco C de 25 lb movendo-se horizontalmente com uma velocidade v 0 colide diretamente com a coluna AB conforme mostrado. Utilizando E = 29 × 10 6p s i , determine a maior velocidade v 0 para que a t