Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 70

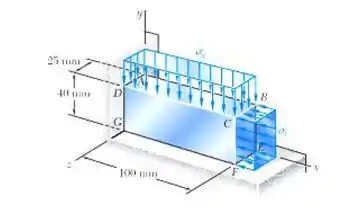
O bloco mostrado na figura é feito de liga de magnésio com E = 34   G P a   e   v = 0,35 . Sabendo que σ x = - 180   M P a , determine (a) a intensidade de σ x para qual a qual a variação na altura do bloco será zero, (b) a variação correspondente na área da face ABCD e (c) a variação correspondente no volume do bloco.

Passo 1

Fala aí gurizada tudo belezinha? O enunciado pede para a gente determinarmos a intensidade de σ x para qual a qual a variação na altura do bloco será zero, então vem comigo :D

  1. δ y = 0       ε y = 0       σ y = 0          

    2. A deformação em Y é dada por:

    ε y = 1 E   x   σ x - v σ y - v σ z

    Para verificarmos a intensidade pedida no enunciado temos que primeiramente determinar a tensão em y:

    σ y = v σ x = 0,35   x   - 180   x   10 6 = - 63   x   10 6   P a

    Agora precisamos determinar a deformação em Z e finalmente em x :D   ε z = 1 E   x   σ z - v σ x - v σ y = v E   x   σ x + σ y = + 1,890   x   10 - 3 ε x = 1 E   x   σ x - v σ y - v σ Z = = σ x - v σ y E = - 157,95   x   10 6 45   x   10 9 = - 3,510   x   10 - 3

    Passo 2

    Para determinarmos a variação correspondente na área da face ABCD, temos que levar em consideração as deformações nas direções que calculamos acima, então vem comigo :D

  2. A 0 = L x L z A = L x 1 + ε x   x   L z   x   1 + ε z = L x L z   x   1 + ε x + ε z + ε x ε z ∆ A = A - A 0 = L x L z   x   ε x + ε z + ε x ε z   ≈   L x L z   x   ε x + ε z

    3. Substituindo os valores temos∶

    ∆ A = 100   m m   x   25   m m   x   ( - 3,510   x   10 - 3 + 1,890   x   10 - 3 ) = - 4,05   m m 2

    Passo 3

    Agora sim, partiu calcular a variação correspondente no volume do bloco, da mesma maneira como a área, temos que levar em consideração as deformações....

  3. V 0 = L x L y L z V = L x 1 + ε x   x   L y   x   1 + ε y   x   L z 1 + ε z   = L x L y L z   x   ε x + ε y + ε z + ε x ε y + ε y ε z + ε z ε x + ε x ε y ε z   ∆ V = V - V 0 = L x L y L z   x   ( ε x + ε y + ε z + p e q u e n o   t e r m o )

Substituindo os valores temos:

∆ V = 100     x   40   x   25   x   ( - 3,510   x   10 - 3 + 0 + 1,890   x   10 - 3 ) = - 162,0   m m ³

Resposta

  1. σ y = - 63,0   M P a
  2. ∆ A = - 4,05   m m 2
  3. ∆ V = - 162,0   m m ³
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste plástica de acrílico tem 200m m de comprimento e 15m m de diâmetro. Se uma carga axial de 300N for aplicada a ela, determine a mudança em seu comprimento e em seu diâmetro. E p = 2,70G P a , v
O bloco é feito de titânio T i - 6 A 1 - 4 V . É submetido a uma compressão de 1,5m m ao longo do eixo y , e sua forma sofre uma inclinação de θ =89,7 ° . Determine ϵ x , ϵ yeγ x y .
As sapatas do freio do pneu de uma bicicleta são feitas de borracha. Se uma força de atrito de 50N for aplicada de cada lado dos pneus, determine a deformação por cisalhamento média na borracha. As di
O tampão tem diâmetro de 30m m e ajusta-se ao interior de uma luva rígida com diâmetro interno de 32m m . Ambos, tampão e luva, têm 50m m de comprimento. Determine a pressão axial p que deve ser aplic
Um suporte isolador de vibração consiste em uma barra A de raio r 1 e um tubo B de raio interno r 2 , colado a um tubo de borracha de 80 mm de comprimento com um módulo de elasticidade transversal G =