Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas Revisão - Ex. 209
As quatro barras mostradas tem a seção transversal de mesma área. Para os carregamentos dados, mostrar que para estas barras: (a) as máximas tensões de compressão obedecem à proporção 4:5:7:9; (b) as máximas tensão de tração obedecem à proporção 2:3:5:3. (Nota: A seção transversal da barra triangular é um tirângulo equilátero.)
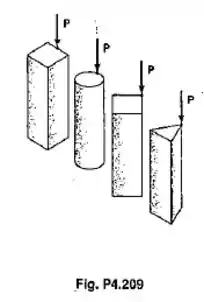
Passo 1
Para analizarmos a tensão de compreção, vamos análizar o ponto que vamos chamar de A, que será exatamente onde a força é aplicada. Para analizarmos a tensão de tração analizamos a outra extremidade, que vou chamar de ponto B.
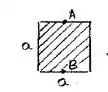
Analisando então o ponto A teremos para a força total
Para o ponto B
Passo 2
Analisando então primeiro o perfil quadrado. A área será dada por
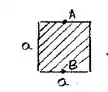
Momento de inércia
Distancia do centro:
E por ultimo
Calculando então a relação para a tensão de compreção (ponto A)
Para a tração (ponto B)
Passo 3
Fazendo a mesma análiza para a seção circular
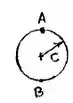
Observa que igualei a por conta do enunciado nos afirmar que todas essas áreas são iguais.
Momento de inércia
Distancia do centro:
Calculando então a relação para a tensão de compreção (ponto A)
Para a tração (ponto B)
Passo 4
Fazendo a mesma análiza para a seção com forma de losango
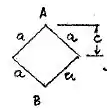
Momento de inércia
Distancia do centro:
E por ultimo
Calculando então a relação para a tensão de compreção (ponto A)
Para a tração (ponto B)
Passo 5
E por ultimo para a seção triangular.
Momento de inércia
Distancia do centro (observe que teremos uma para o ponto A diferente do ponto B):
Calculando então a relação para a tensão de compreção (ponto A)
Para a tração (ponto B)