Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 108
Uma operação de fresagem foi usada para remover parte de uma barra cheia de seção transversal quadrada. Forças de intensidade são aplicados aos centros das extremidades da barra. Sabendo que e , determine a menor dimensão admissível para a parte fresada da barra.
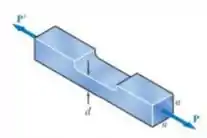
Passo 1
Fala galerinha, nosso objetivo é determinar a máxima carga P que podemos aplicar, sabendo que a nossa seção suporta uma tensão de . Com isso sabemos que o cálculo da tensão é dado por:
Como queremos a carga máxima, vamos considerar tudo sem sinal e essa fórmula aqui de cima como uma soma, assim teremos que:
Sabemos que se tirarmos toda a parte da nossa seção, e levarmos as cargas para lá, teremos o seguinte:
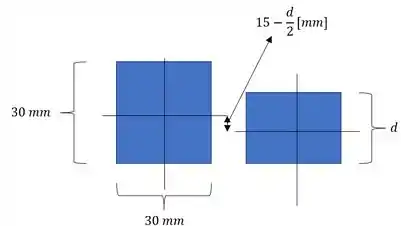
Como a distância entre centroides é de , vamos usar isso para o cálculo do nosso momento, assim temos que:
Passo 2
Vamos definir o momento de inércia, a área e y, assim teremos que:
- (item A)
- Área da seção
- (item A)
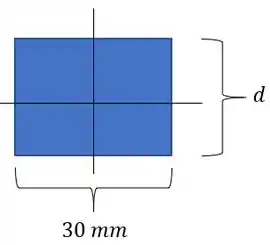
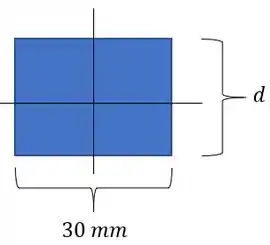
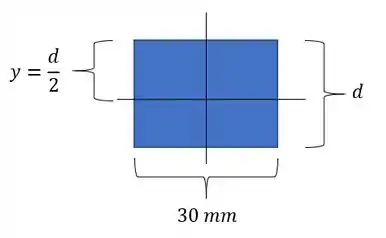
Substituondo na nossa equação temos que:
Substituindo o momento e a carga P tem-se que:
Temos que:
Substituindo teremos que:
Multiplicando tudo por .
Obs: vale lembrar que ignoramos o valor de negativo, como só tivemos um valor positivo, então ficamos com esse valor.