Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 143
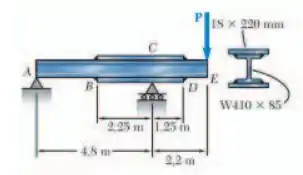
Sabendo que , determine a maior força concentrada que pode ser aplicada na extremidade da viga mostrada.
Passo 1
Fala aí, pessoal. Beleza? Bora zerar esse livro.
a maior força concentrada que pode ser aplicada na extremidade da viga mostrada:
Sabendo disso, vamos calcular a reação de apoio através das equações de equilíbrio:
E também:
Assim, podemos concluir esboçar o diagrama força cortante:
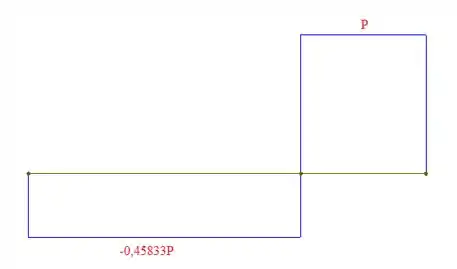
E também o diagrama de momento fletor:
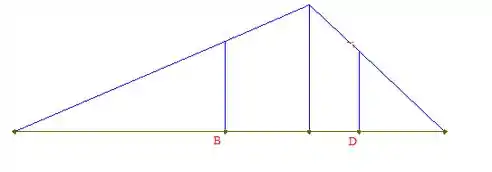
Pelo diagrama, podemos ver que o momento em é maior que o momento em , logo:
Passo 2
Em seguida, já que temos o momento máximoe o enunciado nos forneceu a tensão normal admissível . Então, basta encontrarmos a outra variável da qual a tensão depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:
Onde é o valor mínimo admissível do módulo de resistência da seção da viga. Para o perfil , temos que:
Subsituindo: