Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 65
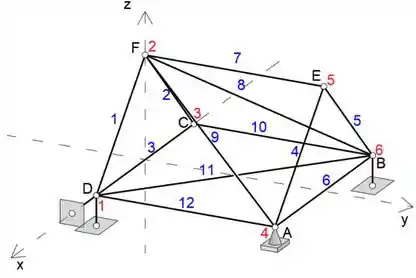
Para a treliça espacial mostrada, verifique a suficiência dos apoios e também a quantidade e disposição das barras para garantir a determinação estática, tanto externa quanto interna. Por inspeção, determine as forças nos membros DC, CB e CF. Calcule a força na barra AF e o componente x da reação na treliça em D.
Passo 1
Verificaremos se a treliça é estaticamente determinada internamente pela equação abaixo
onde m é um número de membros e j número de juntas. Esta treliça contém seis juntas e doze membros
Uma vez que a equação é satisfeita e cada junta tem pelo menos três membros conectados, isso significa que a treliça é determinada estaticamente
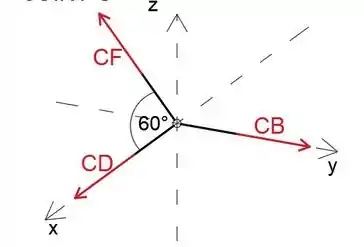
Primeiro, analisaremos a junta C para determinar as forças nos membros CF, CD e BC
Podemos notar que apenas a força CF tem componente z, portanto, ao igualar a soma das forças na direção z a zero, podemos determiná-la
Triângulo △ DCF é equilátero, portanto, o membro CF faz o ângulo de 60∘ com o eixo x
Ao igualar a soma das forças na direção x - e y - a zero, podemos determinar as forças nos membros BC e CD
Passo 2
A partir do diagrama de corpo livre, ao igualar a soma dos momentos em torno do eixo que passa pelo ponto A e é paralelo ao eixo z a zero, a única incógnita será a força DX
Podemos ver que existem quatro forças desconhecidas atuando no ponto F, portanto, devemos primeiro calcular a força no membro EF ou DF
Podemos determinar a força EF analisando a junta E, mas para determinar a força DF, devemos calcular o componente z da força de reação em D a partir do diagrama de corpo livre
Equacionando a soma dos momentos em torno do eixo que passa pelo ponto A e é paralelo ao eixo x a zero, a única incógnita será a força DZ
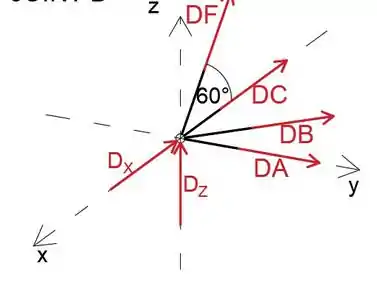
Ao analisar a junta D, podemos notar que apenas a força DF tem componente z, portanto, ao igualar a soma das forças na direção z a zero, podemos determiná-la
Triângulo △ DCF é equilátero, portanto, o membro CF faz o ângulo de 60∘ com o eixo x
Vamos supor que todos os membros estejam em tensão
Passo 3
Agora que determinamos as forças EF e DF, podemos analisar a junta F, uma vez que existem três forças desconhecidas atuando nela
Sabemos que os membros DF e EF estão em compressão, então as forças DF e EF vão em direção ao ponto F
Uma vez que o membro EF é paralelo ao eixo y, podemos escrevê-lo como
Podemos escrever o vetor de força DF como um produto de sua magnitude DF e um vetor unitário de direção de força nD ⃗F
Podemos ver na imagem que as coordenadas dos pontos D e F são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever nD ⃗F como
Passo 4
Podemos escrever o vetor de força FB como um produto de sua magnitude FB e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos F e B são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Podemos escrever o vetor de força FA como um produto de sua magnitude AF e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos A e F são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 5
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos 3 equações de equilíbrio
(1)
(2)
(3)
Multiplique a equação (1) por
(4)
Adicionando as equações (2) e (4) obteremos a equação em que AF é a única incógnita