Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 64
A treliça espacial de Prob. 4/63 é modificado conforme mostrado em que seus suportes e carregamento são alterados. Determine as forças nas barras AC e BD e compare com os resultados do Prob. 4/63.
Passo 1
Podemos ver que existem cinco forças desconhecidas agindo no ponto D e quatro no ponto C, portanto, devemos primeiro determinar as forças de reação em C e D e, em seguida, a força no membro CD do diagrama de corpo livre
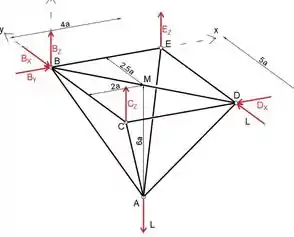
Ao igualar a soma dos momentos sobre o eixo x, podemos determinar a força de reação Cz
Ao igualar a soma dos momentos sobre o eixo z, podemos determinar a força de reação Dx
uma vez que conhecemos a força de reação em C, analisando a junta C, podemos determinar a força no membro CD
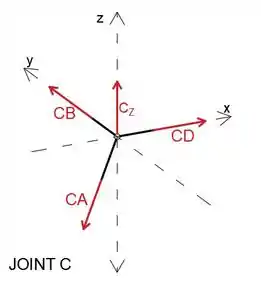
Vamos supor que todos os membros estejam em tensão
Uma vez que as forças CD, CB e C_Z são paralelas aos eixos x, y e z respectivamente, podemos escrevê-los como
Passo 2
Podemos escrever o vetor de força CA como um produto de sua magnitude CA e um vetor unitário de direção de força
Podemos ver no esboço que as coordenadas dos pontos C e A são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Por fim, a expressão para o vetor de força é
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos 3 equações do equilíbrio
(1)
(2)
(3)
Passo 3
Da equação (3), podemos determinar a força no membro AC
Substituindo AC pelo seu valor na equação (1), podemos determinar a força no membro CD
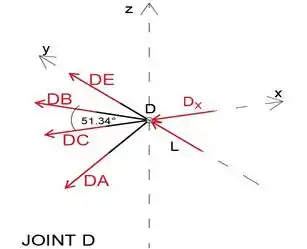
Agora que determinamos as forças CD e Dx, podemos analisar a junta D
Observe que o membro faz com o ângulo do eixo x de
vamos supor que todos os membros estejam em tensão
Podemos notar que o vetor DA é o único com componente z, portanto, ao igualar a soma das forças na direção z a zero fica claro que a força AD é igual a zero
Passo 4
Agora, ao igualar a soma das forças na direção x a zero, podemos determinar a força no membro BD
Substitua CD e Dx por seus valores
Como obtivemos resultado negativo, isso significa que o membro BD está em compressão
Em comparação com os resultados do Prob. 4/63, podemos concluir que os membros são mais estressados quando a força é adicionada à junta D.
Resposta
Em comparação com os resultados do Prob. 4/63, podemos concluir que os membros são mais estressados quando a força é adicionada à junta D