Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 211

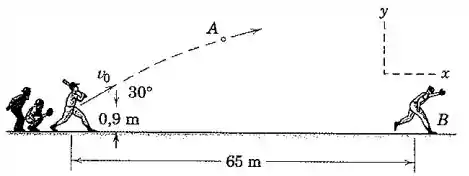
Um rebatedor acerta a bola de beisebol A com uma velocidade inicial de v 0 = 30   m / s diretamente para o jogador B com um ângulo de 30 ° com a horizontal; a posição inicial da bola é 0,9   m acima do nível do solo. O jogador B precisa de 1 4   s para julgar onde a bola deve ser apanhada e começar a se mover para essa posição com velocidade constante. Devido a grande experiência, o jogador B decide sua velocidade de corrida de modo que chegue na “posição de apanhar” simultaneamente com a bola. A posição de apanhar é a localização no campo em que a altura da bola é de 2,1   m . Determine a velocidade da bola em relação ao jogador no instante em que a captura é feita.

Passo 1

Primeiro vamos calcular o tempo total T que a bola demora para chegar à altura de 2,1   m , por meio da equação:

y = y 0 + v 0   s e n   30 °   t - 1 2 g t 2 = 0,9 + 30   s e n   30 °   t - 1 2 9,8 t 2

y = 0,9 + 15   t - 4,9   t 2

2,1 = 0,9 + 15   T - 4,9   T 2

4,9   T 2 - 15   T + 1,2 = 0

T = 0,082   s                     o u                     T = 2,98   s

Consideraremos apenas o maior tempo, T = 2,98   s , pois a outra solução se refere a quando a bola passa pela altura de 2,1   m na subida da trajetória.

Sabendo o valor de T , podemos calcular a velocidade v A da bola quando é capturada pelo jogador:

v A x = v 0 cos ⁡ 30 ° = 30 cos ⁡ 30 ° = 25,98   m / s

v A y = v 0   s e n   30 ° - g T = 30   s e n   30 ° - 9,8 2,98 = - 14,2   m / s

Ou seja,

v A = 25,98   i - 14,2   j

Passo 2

Agora vamos tentar determinar a velocidade v B do jogador. Mas antes, precisamos saber que distância ele precisa correr. Vamos calcular o alcance x da bola a partir da posição do jogador:

x = x 0 + v A x T = - 65 + 25,98 2,98 = 12,42   m

Como ele fica 0,25   s parado antes de começar a correr, sua velocidade deve ser:

v B = x Δ t = 12,42 2,98 - 0,25 = 4,55   m / s

Vetorialmente, isso quer dizer:

v B = 4,55   i + 0   j

Então já podemos obter a velocidade relativa v A B da bola em relação ao jogador, assim:

v A B = v A - v B

v A B = 25,98   i - 14,2   j - 4,55   i + 0   j

v A B = 21,4   i - 14,2   j

Resposta

v A B = 21,4   i - 14,2   j

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O motor em C puxa o cabo com uma aceleração de a c = ( 3 t 2 ) m/s2, onde t é dado em segundos. O motor em D puxa o cabo a a d = 5 m/ s 2 . Se ambos motores partem ao mesmo tempo do repouso quando d=3
Se os motores em A e B recolhem seus cabos conectados com uma aceleração a=0,2t m/s2, onde t é dado em segundos, determine a velocidade escalar do bloco quando ele alcança uma altura de h=4m, partindo
Um motociclista em A está viajando a 18 m/s quando quer passar o caminhão T que está viajando a uma velocidade escalar constante de 18 m/s. Para conseguir isso, o motociclista acelera a 1,8 m/s2 até a
No instante mostrado, carros A e B estão se deslocando com as velocidades escalares mostradas. Se B está acelerando a 1200 km/h2 enquanto A mantem uma velocidade escalar constante, determine a velocid
Dois aviões A e B estão se movendo com as velocidades constantes mostradas. Determine a intensidade e a direção da velocidade do avião B em relação ao avião A .