Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 18
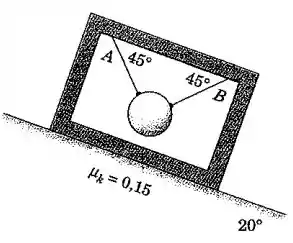
A esfera de aço com está suspensa em uma estrutura de que desliza para baixo no plano inclinado a . Se o coeficiente de atrito dinâmico entre a estrutura e o plano inclinado é , calcule a tração em cada um dos fios de suporte e .
Passo 1
Pessoal, o problema fica menos complicado se a gente considerar o eixo na direção de descida, e o eixo perpendicular a ele. Primeiro, vamos analisar as forças da estrutura que desliza no plano inclinado.
Como a estrutura não voa nem afunda no plano inclinado, as forças no eixo se anulam. Essas forças são a normal e a componente do peso, e portanto,
Agora na direção , vamos aplicar a Segunda Lei de Newton:
onde é a componente do peso que favorece a descida e é a força de atrito dinâmico, oposta à descida:
Substituímos a expressão que encontramos para a normal :
Substituindo e , obtemos a aceleração da estrutura:
Passo 2
Como a esfera de aço está ligada à estrutura, ela também vai adquirir essa mesma aceleração na direção considerada, e permanecerá em equilíbrio na direção :
onde como explicado anteriormente, é a componente da tração na direção e é a componente da tração na direção :
Substituindo as constantes e , obtemos a seguinte equação:
Passo 3
Se também aplicarmos a Segunda Lei de Newton na direção para a esfera, obteremos mais uma equação:
Substituímos de novo as constantes, e também , conforme já calculado:
Então, a gente obteve um sistema de duas equações e duas incógnitas:
cuja solução é: