Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 121

Um recipiente de peso W é sustentado pelo anel A. O cabo BAC passa através do anel e é fixado nos suportes B e C. Duas forças P → = P i → e Q → = Q k → são aplicadas no anel para manter a posição como mostrado na figura. Sabendo que W = 376 N, determine P e Q. (Dica: a tração é a mesma em ambas as porções do cabo BAC.)

Passo 1

Podemos escrever o somatório de forças no ponto A baseado na figura a seguir como:

∑ F → A = 0

T → A B + T → A C + Q k → - W j → + P i → = 0

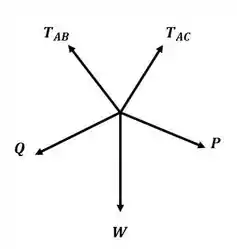
Agora precisamos escrever os vetores tensão em termos de suas coordenadas, para isso, precisamos primeiro escrever o vetor que liga esses pontos, então:

A B → = - 130 i → + 400 j → + 160 k →

A C → = - 150 i → + 400 j → - 240 k →

Agora, calculando o módulo desses vetores:

A B = - 130 2 + 400 2 + 160 2 → A B = 450   m m

A C = - 150 2 + 400 2 + - 240 2 → A C = 490   m m

Agora podemos escrever os vetores tensão (lembrando que o enunciado nos disse que eles possuem o mesmo módulo para a tensão) como:

T → A B = T . A B → A B = T - 13 45 i → + 40 45 j → + 16 45 k →

T → A C = T . A C → A C = T - 15 49 i → + 40 49 j → - 24 49 k →

Passo 2

Agora substituindo os valores das tensões na equação de equilíbrio de forças do passo 1, temos:

T - 13 45 i → + 40 45 j → + 16 45 k → + T - 15 49 i → + 40 49 j → - 24 49 k → + Q k → - W j → + P i → = 0

Agora vamos separar as componentes i → ,   j → e k → :

- 13 45 T - 15 49 T + P = 0

40 45 T + 40 49 T - W = 0

16 45 T - 24 49 T + Q = 0

Agora, substituindo o valor de W dado no enunciado, as equações se tornam:

- 13 45 T - 15 49 T + P = 0

40 45 T + 40 49 T - 376 = 0

16 45 T - 24 49 T + Q = 0

Passo 3

Da segunda equação do passo 2, temos:

40 45 T + 40 49 T - 376 = 0 → T = 220,5   N

Agora, substituindo esse valor na primeira e terceira equação do passo 2:

- 13 45 220,5 - 15 49 220,5 + P = 0 → P = 131,2   N

16 45 220,5 - 24 49 220,5 + Q = 0 → Q = 29,6   N

Resposta

P = 131,2   N

Q = 29,6   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sob a ação do torque de 40N m (acoplamento) aplicado ao eixo vertical, o cabo de restrição A C limita a rotação do braço O A e eixo acoplado a um ângulo de 60 ° medido a partir do eixo y . O colar D f
A lixadeira elétrica tem massa de 3k g com centro de massa em G e é mantida em uma posição ligeiramente inclinada (eixo z vertical) de forma que o disco de lixa faça contato em seu topo A com a superf
A ferramenta mostrada é usada para endireitar membros torcidos quando a estrutura de madeira é concluída. Se a força P = 30l b for aplicada ao cabo conforme mostrado, determine as forças normais aplic
A placa uniforme de 15k g é soldada ao eixo vertical, que é suportado pelos rolamentos A e B . Calcule a magnitude da força suportada pelo rolamento B durante a aplicação do binário de 120N m ao eixo.
Determine uma expressão geral para a força normal N A exercida pela parede vertical lisa na barra esguia e uniforme de massa m e comprimento L . A massa do cilindro é m 1 , e todos os rolamentos são i