Determine uma expressão geral para a força normal exercida pela parede vertical lisa na barra esguia e uniforme de massa e comprimento . A massa do cilindro é , e todos os rolamentos são ideais. Determine o valor de que faz e .

Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar a equação que define a força normal que a parede vertical lisa exerce na barra em . Além disso, determinar a massa do cilindro quando e .

Show de bola! Vamos começar analisando o cilindro separadamente:

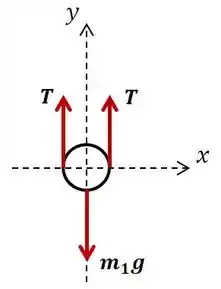
Fazendo o equilíbrio de forças na direção temos:

Ou seja, uma vez que temos rolamentos ideias, a força de tensão no cabo é metade do peso do cilindro. Para encontrarmos a expressão de , vamos isolar a barra e fazer o somatório de forças em torno do rolete que, para manter o equilíbrio, deve ser nulo. Na barra, temos atuando o peso dela em , a força normal em , a tensão do cabo em e as reações em (que não entram no momento e não foram pedidas no enunciado).

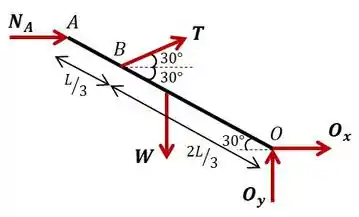
Dica: para os momentos causados por e , apenas utilizamos as distâncias vertical e horizontal, respectivamente, até o ponto . Para , basta multiplicar a componente da força perpendicular à barra (usar ) pela distância . Continuando: