Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 81

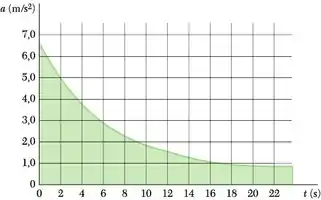
O registro de aceleração mostrado na figura foi obtido durante os testes de velocidade escalar de um carro esportivo. Sabendo que o carro parte do repouso, determine por meios aproximados (a) a velocidade do carro quando t = 8 s, (b) a distância que o carro percorreu quando t = 20 s.

Passo 1

Fala ai pessoal tudo bem?? O enunciado pede que a gente encontre a velocidade do carro quando t = 8 s, (b) a distância que o carro percorreu quando t = 20 s.

Dado:

a - t   curva ;

at   t = 0 ,   x = 0 ,   v = 0

  1. A curva a-t é primeiro aproximada com uma série de retângulos, cada um com largura ∆ t = 2 s. A área ( ∆ t) (amédia) de cada retângulo é aproximadamente igual à mudança na velocidade ∆ v para o intervalo de tempo especificado. Portanto,

    2. ∆ v = a média   ∆ t

    Onde os valores de amédia e ∆ v são dados nas colunas 1 e 2, respectivamente, da tabela a seguir.

    Passo 2

  2. Observando que v0 = 0 e que

    3. v 2 = v 1 + ∆ v 12

    Onde ∆ v12 é a mudança na velocidade entre os tempos t1 e t2, a velocidade no final de cada intervalo de 2 s pode ser calculada; consulte a coluna 3 da tabela e a curva v-t.

    Passo 3

  3. A curva v-t é em seguida aproximada com uma série de retângulos, cada um com largura ∆ t = 2 s. A área ( ∆ t) (vmédia) de cada retângulo é aproximadamente igual à mudança na posição ∆ x para o intervalo de tempo especificado.

    4. Portanto,

    ∆ x = v média   ∆ t

    onde vave e ∆ x são dados nas colunas 4 e 5, respectivamente, da tabela.

    Passo 4

  4. Com x0 = 0 e observando isso

x 2 = x 1 + ∆ x 12

onde ∆ x12 é a mudança na posição entre os tempos t1 e t2, a posição no final de cada intervalo de 2 s pode ser calculada; consulte a coluna 6 da tabela e a curva x-t.

Passo 2

  1. Em

    2. t = 8   s ,             v = 32.58   m/s

    Passo 6

  2. Em

t = 20   s

Resposta

a)   v = 117.3   km/h

b)   660   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que o diâmetro do sol e de 1382 × 10³ km e que a aceleração da gravidade na sua superfície e de 270 m/s2, determine o raio da orbita do planeta indicado em torno do sol considerando que a orbi
A rotação da haste OA em torno de O e definida pela relação θ = (4t2 - 8t), onde θ e t são expressos em radianos e segundos, respectivamente. O cursor B desliza ao longo da haste de tal modo que sua d
Sabendo que o diâmetro do sol e de 1382 × 103 km e que a aceleração da gravidade na sua superfície e de 270 m/s2, determine o raio da orbita do planeta indicado em torno do sol considerando que a orbi
Um satélite vai percorrer indefinidamente uma orbita circular em torno de um planeta se o componente normal da aceleração do satélite for igual a g(R/r)2, onde g e a aceleração da gravidade na superfí
Sabendo que o raio da Terra e 6.370 km, determine o tempo que o telescópio espacial Hubble leva para percorrer uma orbita, considerando que o telescópio percorre uma orbita circular 590 km acima da su