Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 7

Represente graficamente os diagramas de força cortante e momento fletor para o eixo e determine a força cortante e o momento em todo o eixo em função de x. Os mancais em A e B exercem somente reações verticais sobre o eixo.

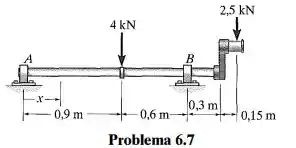
Passo 1

Fazemos o diagrama de corpo livre:

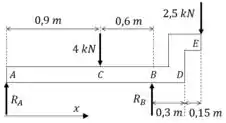
Primeiro vamos substituir a carga desalinhada no ponto E , por uma carga equivalente no ponto D

M D - 2,5 ⋅ 0,15 = 0

M D = 0,375   k N m

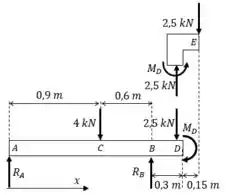
O diagrama de corpo livre resultante é:

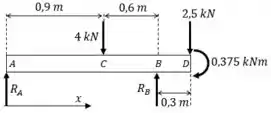
Passo 2

Agora vamos calcular as reações de apoio:

∑ M A = 0 ⇒ - 4 ⋅ 0,9 + R B ⋅ 1,5 - 2,5 ⋅ 1,8 - 0,375 = 0

R B = 4 ⋅ 0,9 + 2,5 ⋅ 1,8 + 0,375 1,5

R B = 5,65   k N m

∑ F y = 0   ⇒ R A - 4 + 5,65 - 2,5 = 0

R A = 0,85   k N m

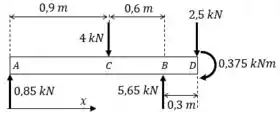
Passo 3

Para desenhar o diagrama de esforço cortante vamos fazer diversas seções na viga e calcular seu comportamento:

Seção AC: 0 ≤ x < 0,9   m

∑ F y = 0 ⇒ - V x + 0,85 = 0

V x = 0,85

∑ M = 0 ⇒ M x - 0,85 x = 0

M x = 0,85 x

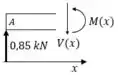
Seção AB: 0,9 ≤ x < 0,15   m

∑ F y = 0 ⇒ - V x + 0,85 - 4 = 0

V x = - 3,15

∑ M = 0 ⇒ M x - 0,85 ⋅ x + 4 ( x - 0,9 ) = 0

M x - 0,85 x + 4 x - 3,6 = 0

M x = - 3,15 x + 3,6

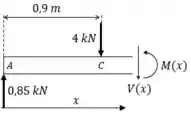
Seção AB: 1,5 ≤ x < 0,18   m

∑ F y = 0 ⇒ - V x + 0,85 - 4 + 5,65 = 0

V x = 2,5

∑ M = 0 ⇒ M x - 0,85 ⋅ x + 4 x - 0,9 + 5,65 ( x - 1,5 ) = 0

M x - 0,85 x + 4 x - 3,6 - 5,65 x + 8,475 = 0

M x = 2,5 x - 4,875

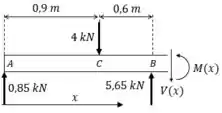
Assim, as equações são:

V x = 0,85 0 ≤ x < 0,9   m - 3,15 0,9 ≤ x < 0,15   m 2,5   1,5 ≤ x < 0,18   m

M x = 0,85 x 0 ≤ x < 0,9   m - 3,15 x + 3,6 0,9 ≤ x < 0,15   m 2,5 x - 4,875 1,5 ≤ x < 0,18   m

Passo 4

Utilizando as equações chegamos nos seguintes gráficos.

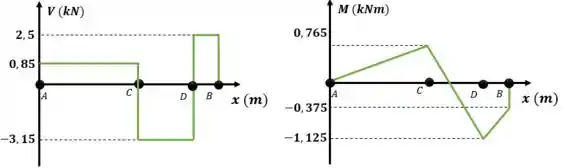
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O guindaste de motores é usado para suportar o motor que pesa 6kN. Represente graficamente os diagramas de força cortante e momento fletor da lança ABC quando ela está na posição horizontal mostrada.
Represente graficamente os diagramas de força cortante e momento fletor para a viga e determine a força cortante e o momento em toda a viga em função de x
A viga está sujeita ao momento uniformemente distribuído m (momento/comprimento). Represente graficamente os diagramas de força cortante e momento fletor para a viga.
Um homem de massa 75 kg está sentado no meio de um barco com largura uniforme e peso de 50 N/m. Determine o momento fletor máximo exercício sobre o barco. Considere que a água exerce uma carga distrib
Represente graficamente os diagramas de força cortante e momento fletor para a viga.