Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 10
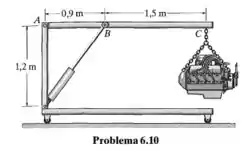
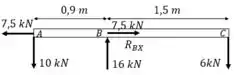
O guindaste de motores é usado para suportar o motor que pesa 6kN. Represente graficamente os diagramas de força cortante e momento fletor da lança ABC quando ela está na posição horizontal mostrada.
Passo 1
Cara, fala aí! Repara que ele só quer que a gente olhe para , então podemos imaginar que isso é uma viga biapoiada, beleza?
Fazemos o diagrama de corpo livre da lança ABC. Observe que nos pontos A e B a conexão é feita por pinos. Isso garante que as únicas reações são de forças em X e Y. Ou seja, não há reação de momento.
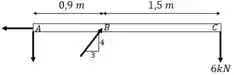
A reação em B pode ser decomposta:
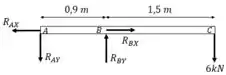
Calculando o somatório dos momentos em e tomando o sentido anti-horário como positivo, temos:
E somando as forças verticais...
Pela relação existente entre as forças em B:
E somando as forças horizontais...
Passo 2
Vamos começar achando as equações do cortante e do momento para as diferentes seções. Aí é colocar as representações dos esforços com conveção positiva dentro da nossa seção e usar as equações de equilíbrio.
Seção AB:
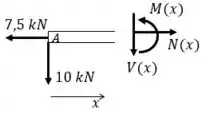
Aí a gente esquece o resto da viga à direita, e foca só nessa parte. Fica assim:
E o somatório de momentos em relação a extremidade direita desse desenhinho:
Passo 3
Seção BC:
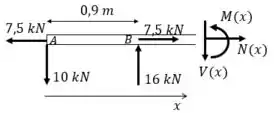
Passo 4
As equações são:
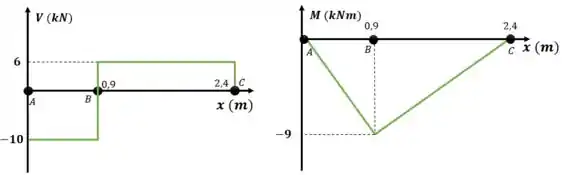
Utilizando as equações podemos traçar os gráficos:
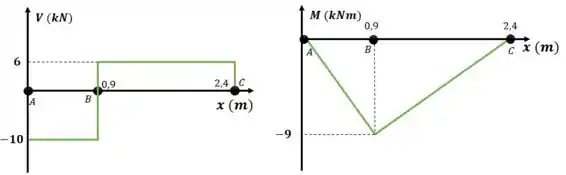
Resposta
