Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 16
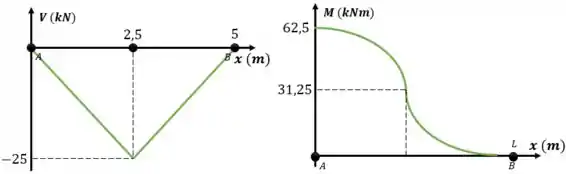
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
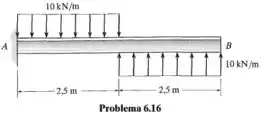
Passo 1
Fala! Essa questão é para a gente fazer os diagramas de momento e cortante dessa viga. Tem um passo a passo para fazer isso. Só seguir, que dá bom!
Primeiro a gente precisa achar as reações no apoio nessa viga engastada:
Vamos fazer um diagrama de corpo livre
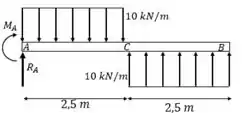
Para facilitar, vamos substituir a carga distribuída por cargas pontuais equivalentes. O valor delas vai ser
E a posição delas é no meio do carregamento distribuído.
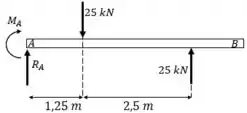
Aplicamos as equações de equilíbrio:
Prontinho. Achamos as reações. Vamos continuar.
Passo 2
Vamos dividir nossa viga em seções. Nossos pontos críticos serão onde começa e onde termina nossos carregamentos distribuídos. Teremos então duas seções.
Para cada intervalo, a gente corta a viga numa seção genérica, distanciada da origem estabelecida por nós mesmos.
O próximo passo é achar as equações do cortante e do momento para as diferentes seções. Aí é colocar as representações dos esforços com convenção positiva dentro da nossa seção e usar as equações de equilíbrio para achar os valores desses esforços.
Só uma observação: aqui a gente volta a usar o carregamento como distribuído, tá?
Seção 1:
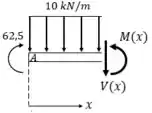
Aqui nossa origem está em . Nós cortamos a viga nesse intervalo, posiocionamos as componentes positivas dos esforços e olhamos só para a parte da viga à esquerda dessa seção.
Fazemos o somatório de momentos na nossa seção
Passo 3
Fazemos o mesmo para a segunda seção:
Seção 2:
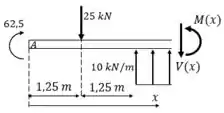
Passo 4
As equações de cortante e momento são:
Às vezes as equações ficam feias, mas para esboçar, você pode achar alguns pontos chave (onde as curvas cortam os eixos coordenados e nos extremos das seções), os valores máximos e mínimos, e se ligar no tipo de curva que precisa fazer.
Utilizando as equações podemos traçar os gráficos:
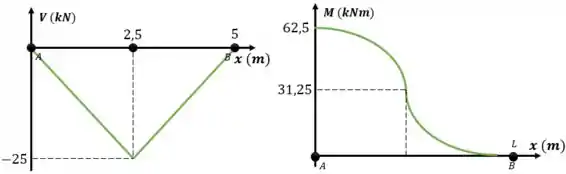
Resposta
