Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 17
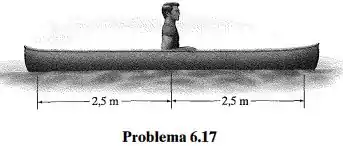
Um homem de massa 75 kg está sentado no meio de um barco com largura uniforme e peso de 50 N/m. Determine o momento fletor máximo exercício sobre o barco. Considere que a água exerce uma carga distribuída uniforme para cima na parte inferior do barco
Passo 1
Fala ai galerinha bonita, tudo beleza?
Saca só, nesse exercício aqui o enunciado nos diz que um homem de está sentado no meio de um barco com largura uniforme e peso de . Sabendo disso ele nos pede para determinar o momento fletor máximo exercido sobre o barco, considerando que a água exerce uma carga distribuída uniforme para cima na parte inferior do barco.
Então belezoca, pra isso vamos começar fazendo o diagrama de corpo livre do barco. Podemos dizer que o homem sentado atua como uma carga pontual, e o empuxo da água gera uma carga distribuída, logo:
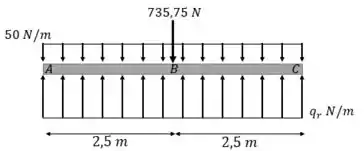
Sendo assim, as forças no eixo serão:
Tal que:
Podemos observar que as cargas distribuídas podem ser somadas vetorialmente, resultando em uma carga resultante , de modo que:
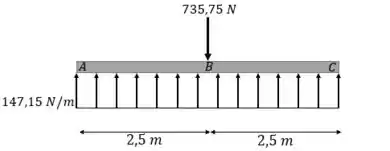
Portanto, o diagrama de corpo livre resultante será dado como:
Passo 2
Iradoso, agora que dispomos das reações de apoio podemos fazer seções no barco para analisar os esforços interno.
Então dada a Seção AB contida no intervalo , teremos que:
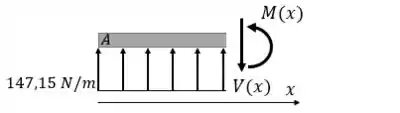
Logo o somatório das forças será:
Enquanto que para o momento, vamos obter que:
Passo 3
Show de bolinhas, agora se a gente pegar a outra seção contida no intervalo , vamos ter que:
Seção AB:
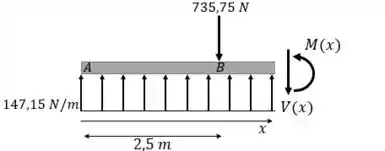
Logo, das forças obtemos que:
Já para o momento, vamos descobrir que:
Portanto, para as duas seções, as equações serão:
Passo 4
Belezoca, agora que temos as equações podemos gerar os seguintes diagramas:
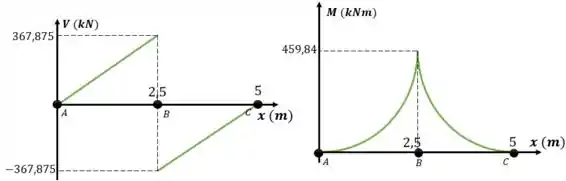
Desse modo, o momento fletor máximo exercicido pelo barco equivale a: