Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 20

Represente graficamente os diagramas de força cortante e momento fletor para a viga e determine a força cortante e o momento em toda a viga em função de x

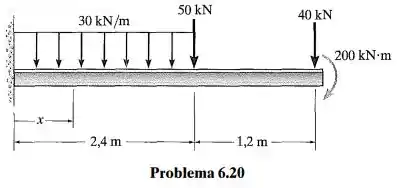
Passo 1

Primeiro desenhamos um diagrama de corpo livre:

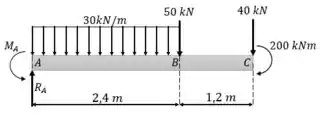
E agora calculamos as reações de apoio:

∑ F Y = - 30 ⋅ 2,4 - 50 - 40 + R A = 0

R A = 162   k N

∑ M A = 0 ⇒ M A - 30 ⋅ 2 , 4 ˙ ⋅ 1,2 - 50 ⋅ 2,4 - 40 ⋅ 3,6 - 200 = 0

M A = 550,4   k N m

Passo 2

Seção AB 0 ≤ x ≤ 2,4 m

∑ F Y = 0 ⇒ 162 - 30 ⋅ x - V x = 0

V x = - 30 x + 162

∑ M = 0 ⇒ 550,4 - 162 x + 30 x ⋅ x 2 + M x = 0

M x = - 15 x 2 + 162 x - 550,4

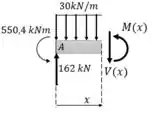
Seção 2,4 < x < 3,6 m

∑ F Y = 0 ⇒ 162 - 30 ⋅ 2,4 - 50 - V x = 0

V x = 40

∑ M = 0 ⇒ 550,4 - 162 x + 30 ⋅ 2,4 ⋅ x - 1,2 + 50 x - 2,4 + M x = 0

550,4 - 162 x + 72 x - 86,4 + 50 x - 120 + M x = 0

M x = 40 x   344

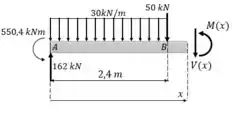
As equações são:

- 30 x + 162 0 ≤ x ≤ 2,4 m 40 2,4 < x < 3,6 m

- 15 x 2 + 162 x - 550,4 0 ≤ x ≤ 2,4 m 40 x - 34 4 2,4 < x < 3,6 m

Passo 3

Com as equações podemos gerar os diagramas

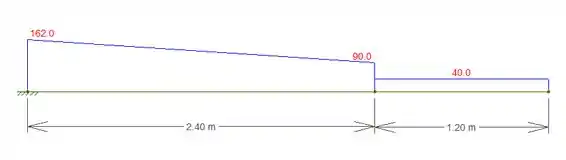
DQ:

DM:

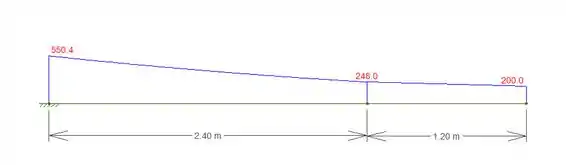
Repara que aqui usamos a conveção de que o diagram de momento é positivo na parte de baixo e negativo na parte de cima, tá?

E assim concluímos a questão!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga suporta a carga distribuída mostrada. Determine as cargas internas resultantes nas seções transversais que passam pelos pontos D e E. Considere que as reações nos apoios A e B sejam verticais.
A força F = 400 N age no dente da engrenagem. Determine as cargas internas resultantes na raiz do dente, isto é, no centroide da seção a-a (ponto A).
A viga suporta a carga distribuída mostrada. Determine as cargas internas resultantes na seção transversal que passa pelo ponto C. Considere que as reações nos apoios A e B sejam verticais.
A lança DF do guindaste giratório e a coluna DE têm peso uniforme de 750 N/m. Se o guindaste e a carga pesam 1.500 N, determine as cargas internas resultantes nas seções transversais que passam nos po
Represente graficamente os diagramas de força cortante e momento fletor para a viga. Os dois segmentos estão interligados em B .