Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 1
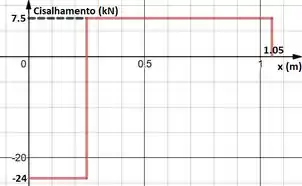
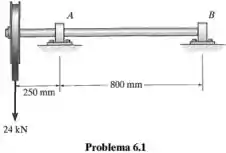
Represente graficamente os diagramas de força cortante e momento fletor para o eixo. Os mancais em A e B exercem somente reações verticais no eixo.
Passo 1
Como toda questão de Resistência, temos que começar de desenhando um diagrama de corpo livre:
Como nosso objetivo é esboçar os gráficos de cortante e momento esse diagrama de corpo livre vai ser o nosso guia, precisamos primeiro encontrar os esforços e substituí-los no diagrama para esboçar os gráficos.
Para isso a gente vai usar as equações de equilíbrio, o ideal é começar pela equação dos momentos escolhendo um bom ponto que elimine incógnitas.
Passo 2
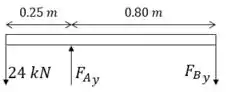
Em posse do diagrama, podemos calcular as reações de apoio. Eu vou escolher o ponto B que elimina a força vertical B.
Considerando o sentido anti-horário positivo pro ponto B a gente tem.
E aí encontramos.
Para encontrar a reação em B, a gente vai usar o somatório das forças verticais.
Considerando pra cima positivo.
E aí:
Enfim esboçando o DCL com os esforços encontrados.
Passo 3
Vamos calcular a equação dos esforços internos da seção OA:
Considerando
Vamos calcular a equação dos esforços internos da seção da viga OB:
Considerando
Passo 4
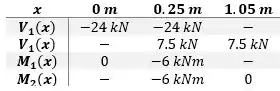
Agora basta utilizar as equações deduzidas acima para traçar os gráficos, obedecendo os limites das equações:
Ao substituir os pontos encontrados na tabela a gente tem.
Resposta
