Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 59

O perfil em U é submetido a um cisalhamento V = 75   k N . Determine o fluxo de cisalhamento máximo no perfil.

Passo 1

Dados da questão: V = 75   k N .

A questão pede o fluxo de cisalhamento máximo no perfil: q m a x _ = ?

Estratégia de resolução: Vamos começar calculando as propriedades geométricas da seção: Centroide, Momento de Inércia. Depois podemos calcular Momento Estático no ponto de interesse. Por fim, usamos a equação de fluxo de cisalhamento para encontrar o q m a x

Passo 2

Primeiro, calculamos o centroide.

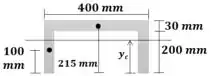
y c = 400 ⋅ 30 ⋅ 215 + 2 ⋅ 200 ⋅ 30 ⋅ 100 400 ⋅ 30 + 2 ⋅ 200 ⋅ 30

y c = 157,5   m m

Passo 3

Agora calculamos o momento de inércia em relação ao centroide

I = 400 ⋅ 30 3 12 + 400 ⋅ 30 ⋅ 57,5 2 + 2 30 ⋅ 200 3 12 + 200 ⋅ 30 ⋅ 57,5 2

I = 120,25 ⋅ 10 6 m m 4

I = 120,25 ⋅ 10 - 6   m 4

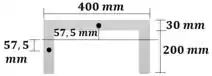
Passo 4

A figura abaixo ilustra o comportamento do fluxo de cisalhamento.

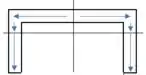
A seção de interesse está destacada abaixo. O fluxo de cisalhamento máximo é encontrado se pegarmos o momento estático de qualquer um dos quadrantes da figura.

Q = 30 ⋅ 157,5 ⋅ 157,5 2

Q = 372093   m m 3

Q = 372,1 ⋅ 10 - 6   m 3

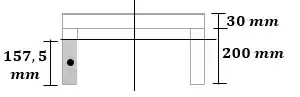
Passo 5

Agora basta aplicar a equação de fluxo de cisalhamento

q m á x = V Q I

q m á x = 75   k N ⋅ 372,1 ⋅ 10 - 6   m 3 120,25 ⋅ 10 - 6   m 4

q m á x = 2 32,08 k N m

Resposta

q m á x = 232,08 k N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Prob. 5.2, considerando que o espaçamento entra os pregos é aumentado para s = 100 mm
Três tábuas, cada uma com 50 mm de espessura, são pregadas juntas para formar uma viga que é submetida a uma força cortante vertical. Sabendo-se que a força de cisalhamento admissível em cada prego é
Três tábuas são pregadas juntas para formar a viga mostrada, que é submetida a uma força cortante vertical. Sabendo-se que o espaçamento entre os pregor é s = 75 mm e que a força de cisalhamento admis
Resolver o Prob. 5.4, considerando que a largura é diminuída para w = 100 mm.
A viga mostrada foi fabricada com dois perfis de aço laminados e duas placas, unidos por parafusos de 20 mm de diâmetro e espaçados longitudinalmente de 190 mm. Determinar a tensão de cisalhamento méd