Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 47
47. Resolva o problema para o ponto localizado na superfície do tubo.
Passo 1
Falaa galerinha! Vamos entender o que ele quer. Ele pede as tensões principais no ponto .
Para achar essas fofas, precisamos achar o estado de tensões nesse ponto. (as tensões que acontecem nesse ponto). E depois calcular as principais através delas.
Precisamos entender que esforços atuam na seção . Para isso, cortamos nosso tubo nessa seção, posicionamos as componentes dos esforços na seção, e olhamos só para parte do tubo a cima dessa seção para determinar o valor dessas componentes.
Vamos montar o diagrama de forças e momentos atuantes no tubo:
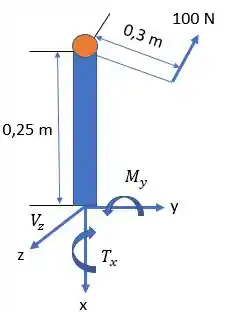
Agora, é só fazer a análise de esforços atuantes na seção do ponto, que é o ponto onde queremos achar as tensões principais:
Os outros esforçam zeram. Vamos seguir!
Passo 2
Agora vamos achar as tensões em , lembrando que a fórmula do momento de inércia de um círculo é da por , onde é a distância do centro até a bora mais externa. Então para a seção de um tubo vazado de raio externo e interno , temos:
A tensão normal vai ser dada só pelo momento, e vai causar tração. Ela é dada por
E é a distância do centro do tubo até o ponto , ou seja, a parte externa do tubo:
Passo 3
Como nosso ponto está na borda superior em relação ao cortante, ele não vai sofrer tensão de cisalhamento por causa dele. Só vamos ter tensão cisalhante por causa da torção:
Novamente temos a seção de um tubo vazado de raio externo e interno .
Uhul! Achamos todas as tensões no ponto .
Passo 4
Agora, é só achar as tensões principais no ponto pela fórmulinha:
Essa fórmula nos permite obter duas tensões, uma máxima e uma mínima .
Vimos que só temos uma tensão normal, e ela é de tração:
Podemos colocar ela no lugar de ou , não vai fazer diferença. E temos uma tensão cisalhante:
Substituindo:
Prontinho!