Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 6
A viga AB é suportada por um pino em A e por um cabo BC. Determine as cargas internas resultantes que agem na seção transversal no ponto D.
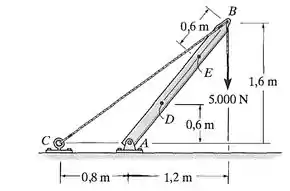
Passo 1
Cara, fala aí! Esse tipo de questão tem um passo a passo muito comum. Só seguir ele que dá bom. A gente quer achar os esforços internos na seção .
Primeiro, a gente vai olhar só para a barra , porque é onde está nossa seção, e vamos fazer o diagrama do corpo livre dela
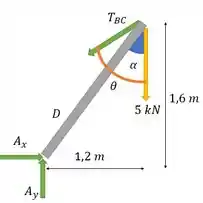
Vamos seguir!
Passo 2
Agora, vamos calcular o momento no ponto para encontrarmos a tração da corda. Para isso, precisamos encontrar o ângulo e o ângulo .
Considerando o sentido anti-horário como positivo
Passo 3
Agora a gente já consegue achar os esforços internos. Por que?
Aí é a parte boa: a gente pode esquecer a parte da barra abaixo da nossa sessão , e olhar só para parte de cima, onde a gente já tem as forças determinadas.
Mas antes, para achar a coordenada do ponto em relação a , precisamos fazer uma semelhança de triângulos:
Partiu fazer o DCL: Vamos colocar as componentes dos nossos esforços na seção .
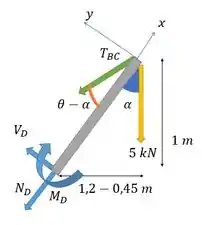
Passo 4
Agora é utilizarmos as equações de equilíbrio e do momento em D para descobrir o valor dessas componentes:
Prontinho!