Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 104

A viga tem seção transversal retangular. Se estiver sujeita a um momento fletor M   =   3.500   N . m direcionado como mostra a figura, determine a tensão de flexão máxima na viga e a orientação do eixo neutro.

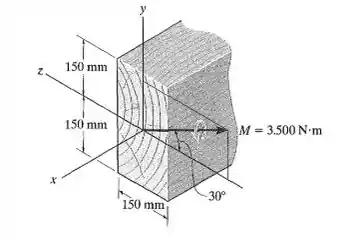
Passo 1

Primeiramente, vamos decompor o momento nos eixos y e z :

M y = 3500 s e n 30 ° = 1750 N m

M z = - 3500 cos ⁡ 30 ° = - 3031,089 N m

Os momentos de inércia serão:

I z = 0,15 × 0,3 3 12 = 3,375 × 10 - 4

I y = ( 0,3 × 0,15 3 0 12 = 8,4375 × 10 - 5

Logo, a tensão será:

σ m á x = σ a = M z y I z + M y z I z = 3031,089 0,15 3,375 × 10 - 4   + 1750 0,075 8,4375 × 10 - 5 = 2,90 M P a

Passo 2

A orientação do eixo neutro será:

t g θ = t g - 30 ° = - 0,5773

t g α = I z I y t g θ

t g α = 3,375 × 10 - 4 8,4375 × 10 - 5 × - 0,5773

α = - 66,6 °

Resposta

σ m á x = 2,90 M P a

α = - 66,6 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para uma viga curva de seção transversal retangular sujeita a um momento fletor M, mostrar que a tensão radial na superfície neutra é: σ r = M A e1 - r 1 R - ln ⁡ R r 1
Sabendo-se que a tensão admissível para a viga mostrada é 80 MPa, determinar o momento fletor admissível M, quando D1 = 150mm, D2 = 180 mm e D3 = 240 mm.
Duas barras de aço são soldadas a uma placa de aço de 3,2 mm de espessura, formando o elemento de máquina mostrado. Sabendo-se que Q=22,5 kN, determinar a maior tensão de tração no elemento .(Dado: Ix
Um momento M atua em um plano vertical e é aplicado a uma viga que tem a seção transversal mostrada. Sabendo-se que E = 200 GPa, determinar as máximas tensões de tração e de compressão e o raio de cur
Duas barras de aço são soldadas a uma placa de aço de 3,2 mm de espessura, formando o elemento de máquina mostrado. Determinar a variação de valores de carga Q, para que a tensão de tração no elemento