Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 24
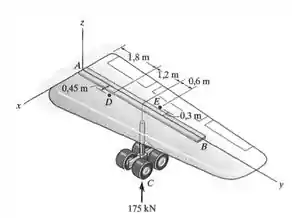
A viga mestra suporta a carga na asa do avião. As cargas consideradas são a reação da roda de em , o peso de do combustível no tanque da asa, com centro de gravidade em D, e o peso de da asa, com centro de gravidade em . Se a viga estiver fixada à fuselagem em A, determine as cargas internas resultantes na viga nesse ponto. Considere que a asa não transfere nenhuma carga à fuselagem, exceto pela viga.
Passo 1
Falaaa, aí! Isso continua sendo uma questão de esforços internos, mas só que em , tá? Mas repara que ele quer os esforços no ponto de reação da nossa viga, em .
Então aqui, o passo de achar as reações e de achar as componentes dos esforços vão se juntar, beleza?
Bora colocar no ponto , as componentes dos esforços internos no 3D: e (que é o esforço normal).
Bora colocar isso no diagrama do corpo livre
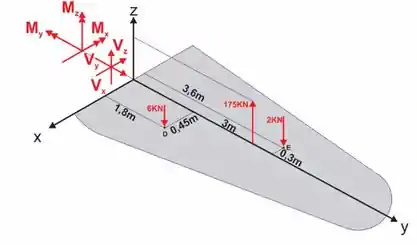
Passo 2
Agora é aplicar as equações de equilíbrio e momento para cada eixo.
Uhul! Arrasamos!