Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 19
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
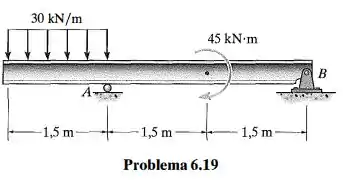
Passo 1
Falaaa galerinha do RespondeAí, tudo belejóia?
Então saca só, nesse exercício aqui o enunciado nos pede para representar graficamente os diagramas de força e momento fletor para a viga. Então quer dizer que precisamos primeiro montar o diagrama de corpo livre da viga e em seguida determinar as equações de esforços internos, porque ai sim, com essas equações em mãos vamos podes montar os diagramas que o enunciado nos pede.
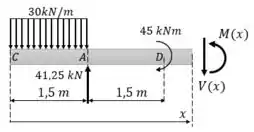
Começamos desenhando um diagrama de corpo livre:
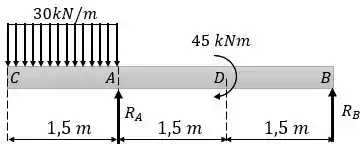
Calculando as reações de apoio, vamos descobrir que:
Logo:
Agora para as forças, vamos descobrir que:
Belezoca, já fizemos uma parte, agora bora lá determinar essas equações de esforços internos!
Passo 2
Iradoso, pra isso vamos fazer sucessivas seções na viga para encontrar as equações de esforços internos, saca só:
Seção CA:
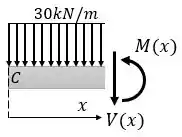
Tal que:
E para o momento:
Passo 3
Agora a outra seção, obtemos:
Seção CD:
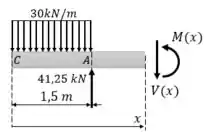
Logo, do somatório das forças:
Enquanto que a soma dos momentos nos diz que:
Passo 4
Belezera, agora para a ultima seção, teremos que:
Seção CB:
Logo, o equilíbrio de forças nos dá:
E a soma dos momentos fornece que:
Portanto, as equações dos esforços internos serão dadas como:
Passo 5
Maravilha, agora que a gente já tem tudo na mão, podemos esboçar os diagramas, tal que:
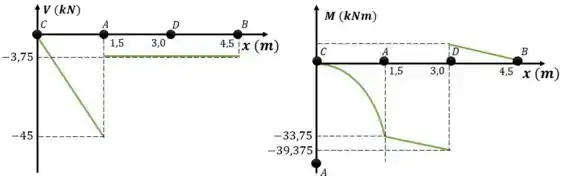
Resposta
Ei, a resposta está no passo a passo :)