Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 1
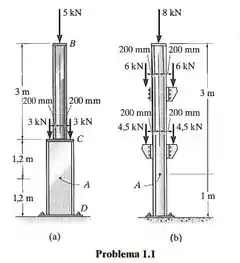
Determine a força normal interna resultante que age na seção transversal no ponto em cada coluna. Em (a), o segmento tem massa de e o segmento tem massa de . Em (b ), a coluna tem uma massa de .
Passo 1
a) Fala aí minha gente, tudo bem com vocês? Bora pra mais essa questão de Resmat.
Ele quer saber a força normal interna resultante no ponto da nossa estrutura. Aí tem um passo a passo para fazer isso. Vamos seguir ele que dá bom. Ah e não se assusta com a figura não, vamos entender ela juntos, bora lá!
Primeira coisa é cortar nossa estrutura em uma seção que passa por , e seja perpendicular a força normal (que a gente quer descobrir), então a seção é horizontal e passa por . E aí a gente posiciona a força normal nela. Aqui vamos colocar ela posicionada para cima.
Depois a gente faz o diagrama de corpo livre desse nosso novo elemento. Ele fica assim:
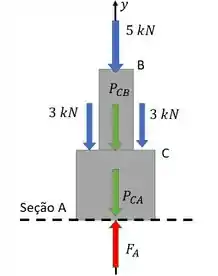
é a força normal interna resultante que a gente quer. E é o peso do segmento e é o peso do segmento . A gente considera eles porque o enunciado diz a massa desses segmentos, tudo bem?
E percebe que quando a gente cortou a nossa estrutura e olhou para cima, o apoio dela sumiu? Por isso que nessa questão a gente não vai precisar achar as reações de apoio.
Passo 2
Agora o que temos que fazer é aplicar a equação de equilíbrio na direção para acharmos a força interna que age em Ou seja:
Quem está para cima a gente coloca positivo no somatório e quem está para baixo fica negativo. Se fizermos isso, teremos:
Aí para achar o peso de cada segmento, como ele dá a massa de como , ou seja, massa por comprimento, a gente precisa multiplicar esse valor pela aceleração da gravidade e pelo comprimento do segmento dado na figura .
Fazemos o mesmo para o segmento que tem :
Substituindo na nossa equação de equilíbrio essas duas expressões:
Substituindo os dados fornecidos, tomando cuidado para calcular os pesos em também, e isolando-se o
Passo 3
b) Para a letra (b), temos o mesmo raciocínio, mas com uma estrutura diferente. Primeiro a gente faz a seção em , coloca a nossa força normal nela e faz o diagrama de corpo livre:
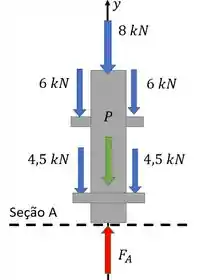
Aqui temos novamente uma coluna que precisamos considerar o peso. Ele diz que a coluna tem uma massa de . Então novamente precisamos multiplicar isso pelo comprimento da coluna até a nossa seção , que é , e por :
Temos então esse peso atuando, a nossa forcinha normal e as forças externas que ele dá.
Passo 4
Agora é fazer o somatório das forças em
Ou seja:
Substituindo:
Percebe que a gente calculou em já. Aí fazendo as continhas: