Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 12

Represente graficamente os diagramas de força cortante e momento fletor para a viga composta interligada por um pino em B

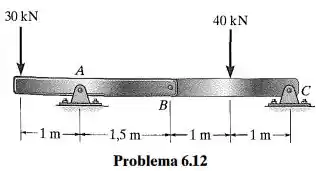
Passo 1

Começamos com o diagrama de corpo livre:

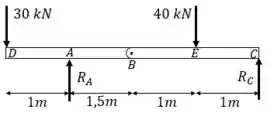
Precisamos garantir que não exista momento interno no ponto B. Então fazemos uma seção neste ponto

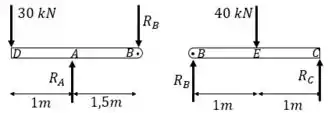
Vamos primeiro utilizar a seção DAB:

∑ M B = 0 ⇒ 30 ⋅ 2,5 - R A ⋅ 1,5 = 0

R A = 50   k N

∑ F y = 0 ⇒ - 30 + R A - R B = 0

R B = 20   k N

Agora utilizando a seção BEC:

∑ F Y = 0 ⇒ R B - 40 + R C = 0

R C = 20   k N

Com essas reações, podemos garantir que não há momento no ponto B

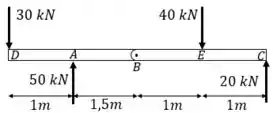
Passo 2

Agora faremos seções na barra para definir as equações:

Seção DA 0 ≤ x ≤ 1

∑ F Y = 0 ⇒ - 30 - V x = 0

V x = - 30   k N

∑ M = 0 ⇒ 30 ⋅ x + M x = 0

M x = - 30 x

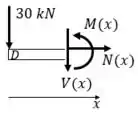
Seção AE 1 ≤ x ≤ 3,5

∑ F Y = 0 ⇒ - 30 + 50 - V x = 0

V x = 20   k N

∑ M = 0 ⇒ 30 ⋅ x - 50 ( x - 1 ) + M x = 0

M x = 20 x - 50

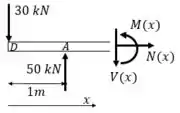
Seção DA 3,5 ≤ x ≤ 4,5

∑ F Y = 0 ⇒ - 30 + 50 - 40 - V x = 0

V x = - 20   k N

∑ M = 0 ⇒ 30 ⋅ x - 50 x - 1 + 40 ( x - 4 ) + M x = 0

M x = - 20 x + 110

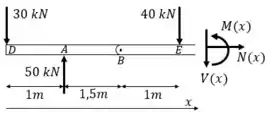
O resulta são as equações:

V x = - 30   k N   0 ≤ x ≤ 1         20   k N 1 ≤ x ≤ 4 - 20   k N 4 ≤ x ≤ 5

M x = - 30 x   0 ≤ x ≤ 1         20 x - 50 1 ≤ x ≤ 3,5 - 20 x + 110 3,5 ≤ x ≤ 4,5

Passo 3

Utilizando as equações podemos gerar os diagramas

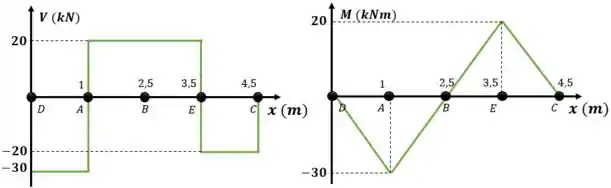
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste curvada AD de raio r tem peso por comprimento w. Se ela estiver no plano horizontal, determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B. Dica: A dist
A haste curvada tem raio r e está presa em B. Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto A, o qual está localizado a um ângulo θ em relação à horizonta
Considere o problema geral de uma viga simplesmente apoiada submetida a n cargas concentras. Escreva um código computacional que possa ser usado para determinar a força cortante interna e o momento em
Faça os diagramas de força cortante e momento fletor para a viga e determine a força cortante e o momento fletor na viga em função de x, onde 0 ≤ x ≤ 1,8m
A viga é feita de um poliéster cuja curva tensão-deformação e mostrada na figura. Se a curva puder ser representada pela equação σ = 140 tg-1(15ε) MPa, onde tg-1(15ε) é dada em radianos, determine o v